题目内容
已知椭圆的中心在原点O,焦点在x轴上,离心率为
,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)若OA⊥OB,求m的值.
| ||
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)若OA⊥OB,求m的值.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆的中心在原点,焦点在x轴上,离心率为
=
,可求得
=
,设椭圆的方程,再把点M(4,1),代入即可;
(Ⅱ)把y=x+m代入椭圆方程,利用OA⊥OB,可得x1x2+y1y2=0,即可求解.
| c |
| a |
| ||
| 2 |
| b |
| a |
| 1 |
| 2 |
(Ⅱ)把y=x+m代入椭圆方程,利用OA⊥OB,可得x1x2+y1y2=0,即可求解.
解答:
解:(Ⅰ)∵
=
,
∴
=
,
依题意设椭圆方程为:
+
=1,把点(4,1)代入,得b2=5,
∴椭圆方程为
+
=1;
(Ⅱ)把y=x+m代入椭圆方程得:5x2+8mx+4m2-20=0,
∵直线l:y=x+m交椭圆于不同的两点A,B,
∴△=64m2-4×5(4m2-20)>0,整理得m2<25,
∴-5<m<5.
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
∴y1y2=(x1+m)(x2+m)=
,
∵OA⊥OB,
∴x1x2+y1y2=
+
=0,
∴m=±2
,满足题意.
| c |
| a |
| ||
| 2 |
∴
| b |
| a |
| 1 |
| 2 |
依题意设椭圆方程为:
| x2 |
| 4b2 |
| y2 |
| b2 |
∴椭圆方程为
| x2 |
| 20 |
| y2 |
| 5 |
(Ⅱ)把y=x+m代入椭圆方程得:5x2+8mx+4m2-20=0,
∵直线l:y=x+m交椭圆于不同的两点A,B,
∴△=64m2-4×5(4m2-20)>0,整理得m2<25,
∴-5<m<5.
设A(x1,y1),B(x2,y2),则x1+x2=-
| 8m |
| 5 |
| 4m2-20 |
| 5 |
∴y1y2=(x1+m)(x2+m)=
| m2-20 |
| 5 |
∵OA⊥OB,
∴x1x2+y1y2=
| 4m2-20 |
| 5 |
| m2-20 |
| 5 |
∴m=±2
| 2 |
点评:本题考查直线与圆锥曲线的关系,着重考查待定系数法求椭圆的方程及方程思想与化归思想,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
用反证法证明:某方程“方程有唯一解”中,假设正确的是该方程( )
| A、无解 | B、有两个解 |
| C、至少两解 | D、至少有两个解或无解 |
△ABC中,a=10,b=14,c=16,则△ABC中的最大角与最小角之和为( )
| A、90° | B、120° |
| C、135° | D、150° |
函数y=x2•cosx的导数为( )
| A、2xcosx+x2sinx |
| B、x2sinx-2xcosx |
| C、2xcosx-x2sinx |
| D、x2cosx-2xsinx |
已知数列{an},满足a1=1,an=3-an-1(n∈N*,n≥2),则a2014=( )
| A、1 | B、2 |
| C、2014 | D、2015 |
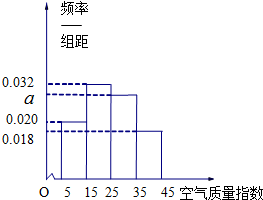 去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.