题目内容
若方程x2cosα-y2sinα+2=0表示一个椭圆，则圆（x+cosα）2+（y+sinα）2=1的圆心在第 象限．
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由已知条件得
，由此得圆（x+cosα）2+（y+sinα）2=1的圆心（-cosα，-sinα）在第四象限．
|
解答：
解：∵方程x2cosα-y2sinα+2=0表示一个椭圆，
∴
，
∴圆（x+cosα）2+（y+sinα）2=1的圆心（-cosα，-sinα）在第四象限．
故答案为：四．
∴
|
∴圆（x+cosα）2+（y+sinα）2=1的圆心（-cosα，-sinα）在第四象限．
故答案为：四．
点评：本题考查圆的圆心所在象限的判断，是基础题，解题时要注意椭圆性质的灵活运用．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
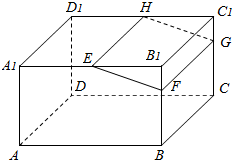如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1，D1C1上的点（点E与B1不重合），且EH∥A1D1，过EH的平面与棱BB1，CC1相交，交点分别为F，G