题目内容
设
，
为非零向量，|
|=2|
|，两组向量
，
，
，
和
，
，
，
，均由2个
和2个
排列而成，若
•
+
•
+
•
+
•
所有可能取值中的最小值为4|
|2，则
与
的夹角为（ ）
| a |
| b |
| b |
| a |
| x1 |
| x2 |
| x3 |
| x4 |
| y1 |
| y2 |
| y3 |
| y4 |
| a |
| b |
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、0 |
考点：数量积表示两个向量的夹角
专题：综合题,平面向量及应用
分析：两组向量
，
，
，
和
，
，
，
，均由2个
和2个
排列而成，结合其数量积组合情况，即可得出结论．
| x1 |
| x2 |
| x3 |
| x4 |
| y1 |
| y2 |
| y3 |
| y4 |
| a |
| b |
解答：
解：由题意，设
与
的夹角为α，
分类讨论可得
①
•
+
•
+
•
+
•
=
•
+
•
+
•
+
•
=10|
|2，不满足
②
•
+
•
+
•
+
•
=
•
+
•
+
•
+
•
=5|
|2+4|
|2cosα，不满足；
③
•
+
•
+
•
+
•
=4
•
=8|
|2cosα=4|
|2，满足题意，此时cosα=
∴
与
的夹角为
．
故选：B．
| a |
| b |
分类讨论可得
①
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| a |
| a |
| b |
| b |
| b |
| b |
| a |
②
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| a |
| a |
| b |
| b |
| a |
| b |
| b |
| a |
| a |
③
| x1 |
| y1 |
| x2 |
| y2 |
| x3 |
| y3 |
| x4 |
| y4 |
| a |
| b |
| a |
| a |
| 1 |
| 2 |
∴
| a |
| b |
| π |
| 3 |
故选：B．
点评：本题考查向量的数量积公式，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，AB是⊙O的直径，P是AB延长线上的一点，过P作⊙O的切线，切点为C，AB=20，∠BAC=30°，AD⊥PC于D，则DE的长为
放在水平桌面上的某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A、π+4 | ||
| B、π+3 | ||
C、
| ||
D、
|
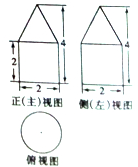
已知某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
| B、3π | ||
C、
| ||
| D、6π |
某个服装店经营某种服装，在某周内获纯利y（元），与该周每天销售这种服装件数x具有线性相关关系，其回归直线方程为
=4.75x+51.36，则下列结论中不正确的是（ ）
 |
| y |
| A、y与x具有正相关关系 | ||||
B、回归直线过样本点的中心（
| ||||
| C、若该周每天销售这种服装件数x增加1件，则获利约增加4.75元 | ||||
| D、若每周每天销售这种服装10件，则可断定获利必为98.86元 |
阅读如图所示的程序框图，则输出的S的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|