题目内容
函数y=logx+1(8-2x)的定义域是( )
| A、(-1,3) |
| B、(0,30 |
| C、(-3,1) |
| D、(-1,0)∪(0,3) |
考点:对数函数的定义域
专题:函数的性质及应用
分析:由对数式的真数大于0,底数大于0且不等于1联立不等式组求解x的取值集合得答案.
解答:
解:由
,得-1<x<0或0<x<3.
∴函数y=logx+1(8-2x)的定义域是(-1,0)∪(0,3).
故选:D.
|
∴函数y=logx+1(8-2x)的定义域是(-1,0)∪(0,3).
故选:D.
点评:本题考查了函数的定义域及其求法,考查了指数不等式的解法,是基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
下表表示一球自一斜面滚下t秒内所行的距离s的呎数(注:呎是一种英制长度单位).
当t=2.5时,距离s为( )
| t | 0 | 1 | 2 | 3 | 4 | 5 |
| s | 0 | 10 | 40 | 90 | 160 | 250 |
| A、45 | B、62.5 |
| C、70 | D、75 |
对于实数x,y,下列各式能将y表示为x的函数的有( )
| A、x3+y3=-27 | ||
| B、x2-y2=1 | ||
| C、xy2=-1 | ||
D、
|
复数z满足|z-1|+|z+1|=
,那么|z|的取值范围是( )
| 5 |
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
| D、[1,2] |
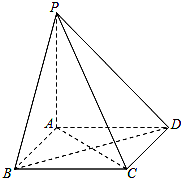 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,且PA=AD.