题目内容
已知集合A={x|x＜a}，B={x|1＜x＜2}，且A∪（∁RB）=R，则实数a的取值范围是（ ）
| A、a≤1 | B、a＜1 |
| C、a≥2 | D、a＞2 |
考点：交、并、补集的混合运算
专题：集合
分析：先求出∁RB，从而根据集合A及A∪（∁RB）=R即可求出a的取值范围．
解答：
解：∵∁RB={x|x≤1，或x≥2}，
∴若A∪（∁RB）=R；
∴a≥2．
故选C．
∴若A∪（∁RB）=R；
∴a≥2．
故选C．
点评：考查描述法表示集合，以及集合的并集、补集运算，也可借助数轴求解．
练习册系列答案
阅读快车系列答案
相关题目
命题“?x∈R，x2≥0”的否定为（ ）
| A、?x∈R，x2＜0 |
| B、?x∈R，x2≥0 |
| C、?x∈R，x2＜0 |
| D、?x∈R，x2≤0 |
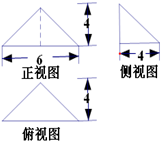若某多面体的三视图（单位：cm），如图所示，其中正视图与俯视图均为等腰三角形，则此多面体的表面积是（ ）cm2．A、5
| ||
B、32+12
| ||
| C、15 | ||
D、5+2
|
已知f（x）为R上的可导函数，且?x∈R，均有f（x）＞f′（x），则有（ ）
| A、e2014f（-2014）＜f（0），f（2014）＞e2014f（0） |
| B、e2014f（-2014）＜f（0），f（2014）＜e2014f（0） |
| C、e2014f（-2014）＞f（0），f（2014）＞e2014f（0） |
| D、e2014f（-2014）＞f（0），f（2014）＜e2014f（0） |
已知点A（-2，0），点B（2，0），若kMA•kMB=-1，则动点M的轨迹方程为（ ）
| A、x2-y2=4（x≠±2） |
| B、x2-y2=4 |
| C、x2+y2=4（x≠±2） |
| D、x2+y2=4 |