题目内容
已知函数f（x）=log4（2x+3-x2），若f（x）=m有两个不同的实数根，求实数m的取值范围．
考点：对数的运算性质
专题：计算题,转化思想
分析：由f（x）=m得到对数方程，化为一元二次方程后直接由判别式大于0得关于m的不等式，求解不等式得m得取值范围．
解答：
解：由f（x）=m，得
log4(-x2+2x+3)=m，
即log4(-x2+2x+3)=log44m，
-x2+2x+3-4m=0，
要使f（x）=m有两个不同的实数根，
则△=22-4×（-1）×（3-4m）＞0，
即4m＜4，解得：m＜1．
∴使f（x）=m有两个不同的实数根的实数m的取值范围是（-∞，1）．
log4(-x2+2x+3)=m，
即log4(-x2+2x+3)=log44m，
-x2+2x+3-4m=0，
要使f（x）=m有两个不同的实数根，
则△=22-4×（-1）×（3-4m）＞0，
即4m＜4，解得：m＜1．
∴使f（x）=m有两个不同的实数根的实数m的取值范围是（-∞，1）．
点评：本题考查对数的运算性质，考查数学转化思想方法，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在数列1，3，6，10，15，x，28中，x的值为（ ）
| A、17 | B、20 |
| C、21 | D、以上都可以 |
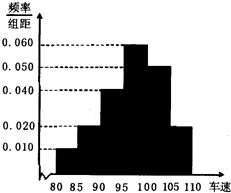2014年春节期间，高速公路车辆剧增．高管局侧控中心在一特定位置从七座以下小型汽车中按先后顺序，每间隔50辆就抽取一辆的抽样方法抽取40辆进行电子测速调查，将它们的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105）．[105，110）后得到如图所示的频率分布直图．