题目内容
14.已知A(1,-2,11),B(6,-1,4),C(4,2,3),则△ABC为( )| A. | 锐角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
分析 利用空间两点间距离公式求出三边长,利用勾股定理能求出△ABC为直角三角形.
解答 解:∵A(1,-2,11),B(6,-1,4),C(4,2,3),
∴|AB|=$\sqrt{(6-1)^{2}+(-1+2)^{2}+(4-11)^{2}}$=5$\sqrt{3}$,
|AC|=$\sqrt{(4-1)^{2}+(2+2)^{2}+(3-11)^{2}}$=$\sqrt{89}$,
|BC|=$\sqrt{(4-6)^{2}+(2+1)^{2}+(3-4)^{2}}$=$\sqrt{14}$,
∴AB2+BC2=AC2,∴AB⊥BC.
∴△ABC为直角三角形.
故选:C.
点评 本题考查三角形形状的判断,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
4.下列式子中表示正确的是( )
| A. | 2+cosx=4 | B. | $\sqrt{10}$>π | C. | sinx•cosx=sin2x | D. | sin75°>cos14° |
3.设全集U={1,2,3,4,5},A={1,5},B={2,4},则B∩(∁UA)=( )
| A. | {2,3,4} | B. | {2} | C. | {2,4} | D. | {1,3,4,5} |
4.方程lnx=$\frac{x+1}{x-1}$实数根的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
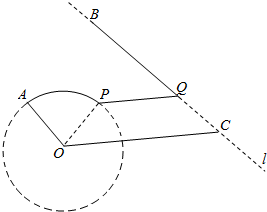 如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.
如图,B、C是海岸线l上相距50km的两个海边小城,圆O是半径为10km的某海岛小城的环岛路,A为圆O上的物资中转站,其中∠AOC=$\frac{2}{3}$π,OC=25km,且l∥OA,为使中转站A的物资运往B城,计划从A地沿环岛路至某地P,再沿水路PQ至海岸线l上Q,最后沿海岸线QB至B城修建运输线,其中PQ∥OC,Q在线段BC上.