题目内容
19.已知函数f(x)定义域为R,则命题p:“函数f(x)为偶函数”是命题q:“?x0∈R,f(x0)=f(-x0)”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据函数奇偶性的定义结合充分条件和必要条件的定义进行判断即可.
解答 解:若函数f(x)为偶函数,则?x∈R,f(-x)=f(x),则?x0∈R,f(x0)=f(-x0)成立,则充分性成立,
若f(x)=x2,-1≤x≤2,满足f(-1)=f(1),但函数f(x)不是偶函数,故必要性不成立,
即p是q的充分不必要条件,
故选:A.
点评 本题主要考查充分条件和必要条件的判断,根据充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.己知A(x1,0),B(x2,1)在函数f(x)=2sin(ωx+φ)(ω>0)的图象上,|x1-x2|的最小值$\frac{π}{4}$,则ω=( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | l | D. | $\frac{2}{3}$ |
8.数学活动小组由12名同学组成,现将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案有( )种.
| A. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{3}^{3}}$A${\;}_{4}^{4}$ | B. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$34 | ||
| C. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{4}^{4}}$43 | D. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$43 |
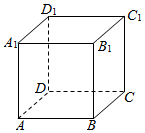 如图,正方体ABCD-A1B1C1D1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积.
如图,正方体ABCD-A1B1C1D1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积. 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: