题目内容
9.复数z1=2sin$θ-\sqrt{3}i$,z2=1+(2cosθ)i,i为虚数单位,θ∈[$\frac{π}{3},\frac{π}{2}$];(1)若z1•z2是实数,求cos2θ的值;
(2)若复数z1、z2对应的向量分别是$\overrightarrow{a}$、$\overrightarrow{b}$,存在θ使等式($λ\overrightarrow{a}-\overrightarrow{b}$)•($\overrightarrow{a}-λ\overrightarrow{b}$)=0成立,求实数λ的取值范围.
分析 (1)利用复数的乘法化简复数,通过复数是实数求出θ,然后求解即可;
(2)写出复数z1,z2对应的向量,代入等式($λ\overrightarrow{a}-\overrightarrow{b}$)•($\overrightarrow{a}-λ\overrightarrow{b}$)=0,展开数量积即可求得实数λ的取值范围.
解答 解:复数z1=2sin$θ-\sqrt{3}i$,z2=1+(2cosθ)i,i为虚数单位,θ∈[$\frac{π}{3},\frac{π}{2}$].
(1)z1•z2=2sinθ+2$\sqrt{3}$cosθ+(4sinθcosθ-$\sqrt{3}$)i,
z1•z2为实数,可得4sinθcosθ-$\sqrt{3}$=0,sin2θ=$\frac{\sqrt{3}}{2}$,
解得2θ=$\frac{2π}{3}$,
∴cos2θ=-$\frac{1}{2}$;
(2)复数z1=2sinθ-$\sqrt{3}$i,z2=1+(2cosθ)i,
复数z1,z2对应的向量分别是$\overrightarrow{a},\overrightarrow{b}$,
$\overrightarrow{a}$=(2sinθ,-$\sqrt{3}$),$\overrightarrow{b}$=(1,2cosθ),
($λ\overrightarrow{a}-\overrightarrow{b}$)•($\overrightarrow{a}-λ\overrightarrow{b}$)=0,
∵${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$=(2sinθ)2+(-$\sqrt{3}$)2+1+(2cosθ)2=8,
$\overrightarrow{a}•\overrightarrow{b}$=(2sinθ,-$\sqrt{3}$)•(1,2cosθ)=2sinθ-2$\sqrt{3}$cosθ,
∴($λ\overrightarrow{a}-\overrightarrow{b}$)•($\overrightarrow{a}-λ\overrightarrow{b}$)=λ(${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}$)-(1+λ2)$\overrightarrow{a}•\overrightarrow{b}$=8λ-(1+λ2)(2sinθ-2$\sqrt{3}$cosθ)=0,
化为sin(θ-$\frac{π}{3}$)=$\frac{2λ}{1+{λ}^{2}}$,
∵θ∈[$\frac{π}{3},\frac{π}{2}$],
∴(θ-$\frac{π}{3}$)∈[0,$\frac{π}{6}$],∴sin(θ-$\frac{π}{3}$)∈[0,$\frac{1}{2}$].
∴0≤$\frac{2λ}{1+{λ}^{2}}$≤$\frac{1}{2}$,解得λ≥2+$\sqrt{3}$或λ≤2-$\sqrt{3}$.
实数λ的取值范围是(-∞,2-$\sqrt{3}$]∪[2+$\sqrt{3}$,+∞).
点评 本题考查复数代数形式的乘除运算,考查复数为实数的条件,训练了向量的数量积的应用,是中档题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | ($\frac{1}{e}$,+∞) | B. | (0,$\frac{1}{e}$) | C. | (-$\frac{1}{e}$,+∞) | D. | (-$\frac{1}{e}$,0) |
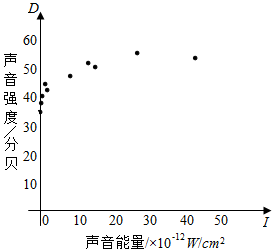 噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{I}$ | $\overline{D}$ | $\overline{W}$ | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)2 | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)2 | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)(Di-$\overline{D}$) | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)(Di-$\overline{D}$) |
| 1.04×10-11 | 45.7 | -11.5 | 1.56×10-21 | 0.51 | 6.88×10-11 | 5.1 |
(Ⅰ)根据表中数据,求声音强度D关于声音能量I的回归方程D=a+blgI;
(Ⅱ)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点P共受到两个
声源的影响,这两个声源的声音能量分别是I1和I2,且$\frac{1}{I_1}+\frac{1}{I_2}={10^{10}}$.已知点P的声音
能量等于声音能量Il与I2之和.请根据(I)中的回归方程,判断P点是否受到噪声污染的干
扰,并说明理由.
附:对于一组数据(μl,ν1),(μ2,ν2),…(μn,νn),其回归直线ν=α+βμ的斜率和截距的最小二乘估计分别为:β=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({u}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\overline{α}$=$\overline{v}$-β$\overline{u}$.
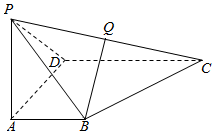 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.