题目内容
8.数学活动小组由12名同学组成,现将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组选出一名组长,则不同的分配方案有( )种.| A. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{3}^{3}}$A${\;}_{4}^{4}$ | B. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$34 | ||
| C. | $\frac{{C}_{12}^{3}{C}_{9}^{3}{C}_{6}^{3}}{{A}_{4}^{4}}$43 | D. | C${\;}_{12}^{3}$C${\;}_{9}^{3}$C${\;}_{6}^{3}$43 |
分析 先分组,再分配,最后选组长,根据分步计数原理可得.
解答 解:将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题有C123C93C63C33,最后选一名组长各有3种,
故不同的分配方案为:C123C93C6334,
故选:B.
点评 本题考查排列、组合的应用,分组分配问题,进行分组分析时要特别注意是否为平均分组,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.在等比数列{an}中,已知a4=27a3,则$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{4}}{{a}_{2}}$+$\frac{{a}_{6}}{{a}_{3}}$+…+$\frac{{a}_{2n}}{{a}_{n}}$等于( )
| A. | $\frac{{3}^{-n}-3}{2}$ | B. | $\frac{{3}^{1-n}-3}{2}$ | C. | $\frac{{3}^{n}-3}{2}$ | D. | $\frac{{3}^{n+1}-3}{2}$ |
19.已知函数f(x)定义域为R,则命题p:“函数f(x)为偶函数”是命题q:“?x0∈R,f(x0)=f(-x0)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
(Ⅰ)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(Ⅱ)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m-n,求随机变量ξ的分布列及其数学期望.
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| (x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(Ⅱ)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m-n,求随机变量ξ的分布列及其数学期望.
18.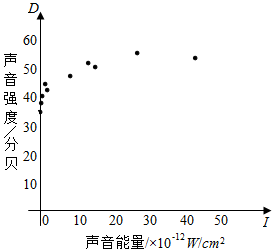 噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.
表中Wi=lgIi,$\overline{W}$=$\frac{1}{10}$$\sum_{i=1}^{10}$Wi
(Ⅰ)根据表中数据,求声音强度D关于声音能量I的回归方程D=a+blgI;
(Ⅱ)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点P共受到两个
声源的影响,这两个声源的声音能量分别是I1和I2,且$\frac{1}{I_1}+\frac{1}{I_2}={10^{10}}$.已知点P的声音
能量等于声音能量Il与I2之和.请根据(I)中的回归方程,判断P点是否受到噪声污染的干
扰,并说明理由.
附:对于一组数据(μl,ν1),(μ2,ν2),…(μn,νn),其回归直线ν=α+βμ的斜率和截距的最小二乘估计分别为:β=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({u}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\overline{α}$=$\overline{v}$-β$\overline{u}$.
 噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.
噪声污染已经成为影响人们身体健康和生活质m的严重问题,为了了解强度D(单位:分贝)与声音能量I(单位:W/cm2)之间的关系,将测量得到的声音强度Di和声音能量Ii(i=1.2.…,10)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{I}$ | $\overline{D}$ | $\overline{W}$ | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)2 | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)2 | $\sum_{i=1}^{10}$(Ii-$\overline{I}$)(Di-$\overline{D}$) | $\sum_{i=1}^{10}$(Wi-$\overline{W}$)(Di-$\overline{D}$) |
| 1.04×10-11 | 45.7 | -11.5 | 1.56×10-21 | 0.51 | 6.88×10-11 | 5.1 |
(Ⅰ)根据表中数据,求声音强度D关于声音能量I的回归方程D=a+blgI;
(Ⅱ)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点P共受到两个
声源的影响,这两个声源的声音能量分别是I1和I2,且$\frac{1}{I_1}+\frac{1}{I_2}={10^{10}}$.已知点P的声音
能量等于声音能量Il与I2之和.请根据(I)中的回归方程,判断P点是否受到噪声污染的干
扰,并说明理由.
附:对于一组数据(μl,ν1),(μ2,ν2),…(μn,νn),其回归直线ν=α+βμ的斜率和截距的最小二乘估计分别为:β=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({u}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,$\overline{α}$=$\overline{v}$-β$\overline{u}$.
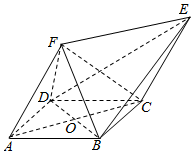 如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.
如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.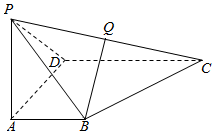 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.