题目内容
在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a=3,∠B=2∠A,cosA=
,则b= .
| ||
| 3 |
考点:正弦定理
专题:解三角形
分析:由条件利用同角三角函数的基本关系,二倍角公式求得sinA和sinB的值,再利用正弦定理求得b的值.
解答:
解:△ABC中,由cosA=
,∠B=2∠A,可得sinA=
,sinB=sin2A=2sinAcosA=2×
×
=
.
再由正弦定理可得
=
,即
=
,求得b=2
,
故答案为:2
.
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
再由正弦定理可得
| a |
| sinA |
| b |
| sinB |
| 3 | ||||
|
| b | ||||
|
| 6 |
故答案为:2
| 6 |
点评:本题主要考查正弦定理、同角三角函数的基本关系,二倍角公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若二项式(x+
)7的展开式中
的系数与
的系数之比是35:21,则a=( )
| a |
| x |
| 1 |
| x |
| 1 |
| x3 |
| A、1 | B、2 | C、-1 | D、-2 |
 在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C、E的动点,则下列说法正确的有( )
在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C、E的动点,则下列说法正确的有( )①直线DE与平面ABF平行;
②当F为CE的中点时,BF⊥平面CDE;
③存在点F使得直线BF与AC平行;
④存在点F使得DF⊥BC.
| A、1个 | B、2个 | C、3个 | D、4个 |
在区间[-
,
]上随机取一个数x,则cosπx的值介于
与
之间的概率为( )
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
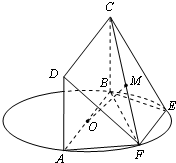 如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.
如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.