题目内容
已知三棱锥P-ABC的所有棱长都等于1,则三棱锥P-ABC的内切球的表面积 .
考点:球的体积和表面积,球内接多面体
专题:计算题,空间位置关系与距离
分析:求出三棱锥P-ABC的高为
=
,利用三棱锥P-ABC的外接球与内切球的半径的比为3:1,可得三棱锥P-ABC的内切球的半径,即可求出三棱锥P-ABC的内切球的表面积.
1-
|
| ||
| 3 |
解答:
解:∵三棱锥P-ABC的所有棱长都等于1,
∴底面外接圆的半径为
,
∴三棱锥P-ABC的高为
=
,
∵三棱锥P-ABC的外接球与内切球的半径的比为3:1,
∴三棱锥P-ABC的内切球的半径为
,
∴三棱锥P-ABC的内切球的表面积为4π×(
)2=
.
故答案为:
.
∴底面外接圆的半径为
| ||
| 3 |
∴三棱锥P-ABC的高为
1-
|
| ||
| 3 |
∵三棱锥P-ABC的外接球与内切球的半径的比为3:1,
∴三棱锥P-ABC的内切球的半径为
| ||
| 12 |
∴三棱锥P-ABC的内切球的表面积为4π×(
| ||
| 12 |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查三棱锥P-ABC的内切球的表面积,考查学生的计算能力,确定三棱锥P-ABC的内切球的半径是关键.

练习册系列答案
相关题目
定义max{a,b}=
,设实数x,y满足约束条件
,则z=max{4x+y,3x-y}的取值范围是( )
|
|
| A、[-8,10] |
| B、[-7,10] |
| C、[-6,8] |
| D、[-7,8] |
已知实数x,y满足
,则z=4x+y的取值范围是( )
|
| A、[0,2] |
| B、[0,8] |
| C、[2,8] |
| D、[2,10] |
执行如图所示的程序框图,则输出的结果是( )


| A、225 | B、75 |
| C、275 | D、300 |
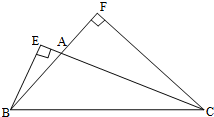 如图,BE、CF分别为钝角△ABC的两条高,已知AE=1,AB=3,CF=4
如图,BE、CF分别为钝角△ABC的两条高,已知AE=1,AB=3,CF=4