题目内容
已知n=
(2x+1)dx,数列{
}的前n项和为Sn,数列{bn}的通项公式为bn=n-35,n∈N*,则bnSn的最小值为______.
| ∫ | n0 |
| 1 |
| an |
an=
(2x+1)dx=(x2+x)
=n2+n
∴
=
=
-
∴数列{
}的前n项和为Sn=
+
+…+
=1-
+
-
+…+
-
=1-
=
,
bn=n-35,n∈N*,
则bnSn=
×(n-35)=n+1+
-37≥2×6-37=-25,
等号当且仅当n+1=
,即n=5时成立,
故bnSn的最小值为-25.
故答案为:-25
| ∫ | n0 |
| | | n0 |
∴
| 1 |
| an |
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
∴数列{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
bn=n-35,n∈N*,
则bnSn=
| n |
| n+1 |
| 36 |
| n+1 |
等号当且仅当n+1=
| 36 |
| n+1 |
故bnSn的最小值为-25.
故答案为:-25

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
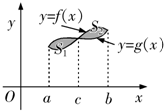
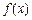 是二次函数,已知
是二次函数,已知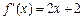 ,且
,且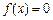 有两个相等实根.问是否存在一个常数
有两个相等实根.问是否存在一个常数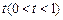 ,使得直线
,使得直线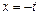 将函数
将函数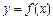 的图象与坐标轴所围成的图形分成面积相等的两部分,若不存在,请说明理由;若存在,则求出此常数
的图象与坐标轴所围成的图形分成面积相等的两部分,若不存在,请说明理由;若存在,则求出此常数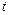 .
.
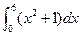 =
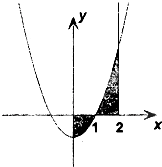
= 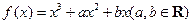 的图象,如图所示,它与直线
的图象,如图所示,它与直线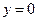 在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为
在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为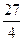 ,则
,则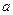 的值为 .
的值为 .