题目内容
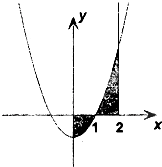
如图,由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积为( )
A.
| B.1 | C.2 | D.3 |

由曲线y=x2-1,直线x=0,x=2和x轴围成的封闭图形的面积为
S=∫01(1-x2)dx+∫12(x2-1)dx
=(x-
x3)|01+(
x3-x)|12
=
+
-2-
+1
=2
故选C.
S=∫01(1-x2)dx+∫12(x2-1)dx
=(x-
| 1 |
| 3 |
| 1 |
| 3 |
=
| 2 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
=2
故选C.

练习册系列答案
相关题目


 ;②
;② ;③
;③ .
.
 与抛物线
与抛物线 所围成的图形面积为S,它们与直线
所围成的图形面积为S,它们与直线 围成的面积为T, 若U=S+T达到最小值,求
围成的面积为T, 若U=S+T达到最小值,求 值;并求此时平面图形绕
值;并求此时平面图形绕 轴一周所得旋转体的体积.
轴一周所得旋转体的体积.