题目内容
(1)当a=
时,解不等式ax2+2x+1>0;
(2)当a∈R时,解关于x的不等式ax2+2x+1>0.
| 1 |
| 2 |
(2)当a∈R时,解关于x的不等式ax2+2x+1>0.
考点:其他不等式的解法
专题:分类讨论,不等式的解法及应用
分析:(1)直接利用一元二次不等式的解法进行求解即可;
(2)对参数a的取值范围进行讨论,根据开口方向分a=0,a>0,a<0三类,当a>0时还需讨论判别式,然后解不等式即可.
(2)对参数a的取值范围进行讨论,根据开口方向分a=0,a>0,a<0三类,当a>0时还需讨论判别式,然后解不等式即可.
解答:
解:(1)当a=
时,不等式为x2+4x+2>0,
∴原不等式的解集为{x|x<-2-
或x>-2+
};
(2)当a=0时,原不等式的解集为{x|x>-
},
当a>0时,方程ax2+2x+1=0,△=4-4a,
①若△>0,即0<a<1时,方程ax2+2x+1=0的两个解为x1=
,x2=
,且x1<x2,
∴原不等式的解集为{x|x<
或x>
};
②若△=0,即a=1时,原不等式的解集为{x|x≠-1};
②若△<0,即a>1时,原不等式的解集为R;
当a<0时,一定有△>0,方程ax2+2x+1=0的两个解为x1=
,x2=
,且x1>x2,
∴原不等式的解集为{x|
<x<
}.
| 1 |
| 2 |
∴原不等式的解集为{x|x<-2-
| 2 |
| 2 |
(2)当a=0时,原不等式的解集为{x|x>-
| 1 |
| 2 |
当a>0时,方程ax2+2x+1=0,△=4-4a,
①若△>0,即0<a<1时,方程ax2+2x+1=0的两个解为x1=
-1-
| ||
| a |
-1+
| ||
| a |
∴原不等式的解集为{x|x<
-1-
| ||
| a |
-1+
| ||
| a |
②若△=0,即a=1时,原不等式的解集为{x|x≠-1};
②若△<0,即a>1时,原不等式的解集为R;
当a<0时,一定有△>0,方程ax2+2x+1=0的两个解为x1=
-1-
| ||
| a |
-1+
| ||
| a |
∴原不等式的解集为{x|
-1+
| ||
| a |
-1-
| ||
| a |
点评:本题考查一元二次不等式的解法,解题的关键是对参数的范围进行分类讨论,分类解不等式,此题是一元二次不等式解法中的难题,易因为分类不清与分类有遗漏导致解题失败,解答此类题时要严谨,避免考虑不完善出错.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
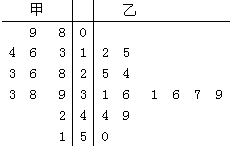 已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )
已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )| A、甲篮球运动员比赛得分更稳定,中位数为26 |
| B、甲篮球运动员比赛得分更稳定,中位数为27 |
| C、乙篮球运动员比赛得分更稳定,中位数为31 |
| D、乙篮球运动员比赛得分更稳定,中位数为36 |
下列各数中最小的一个是( )
| A、111111(2) |
| B、210(6) |
| C、1000(4) |
| D、101(8) |
 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-