题目内容
设偶函数f(x)对任意x∈R都有f(x)=-
且当x∈[-3,-2]时f(x)=4x,则f(119.5)=( )
| 1 |
| f(x-3) |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
考点:函数的周期性
专题:函数的性质及应用
分析:先根据条件求出函数的周期,然后根据周期进行化简得f(119.5)=f(-0.5),再根据奇偶性和条件将-0.5转化到区间[-3,-2]上,代入解析式可求出所求.
解答:
解:∵函数f(x)对任意x∈R都有f(x)=-
,
∴f(x+3)=-
,
则f(x+6)=f(x),
即函数f(x)的周期为6,
∴f(119.5)=f(20×6-0.5)=f(-0.5)=-
=-
,
又∵偶函数f(x),
当x∈[-3,-2]时,有f(x)=4x,
∴f(119.5)=-
=-
=-
=
.
故选:C.
| 1 |
| f(x-3) |
∴f(x+3)=-
| 1 |
| f(x) |
则f(x+6)=f(x),
即函数f(x)的周期为6,
∴f(119.5)=f(20×6-0.5)=f(-0.5)=-
| 1 |
| f(-0.5+3) |
| 1 |
| f(2.5) |
又∵偶函数f(x),
当x∈[-3,-2]时,有f(x)=4x,
∴f(119.5)=-
| 1 |
| f(2.5) |
| 1 |
| f(-2.5) |
| 1 |
| 4×(-2.5) |
| 1 |
| 10 |
故选:C.
点评:本题主要考查了函数的奇偶性和周期性,要特别利用好题中有f(x)=-
的关系式.在解题过程中,条件f(x+a)=-
通常是告诉我们函数的周期为2a.属于中档题.
| 1 |
| f(x-3) |
| 1 |
| f(x) |

练习册系列答案
相关题目
实数x,y满足x+y-4=0,则 x2+y2的最小值是( )
| A、8 | ||
| B、4 | ||
C、2
| ||
| D、2 |
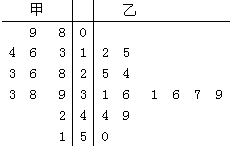 已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )
已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )| A、甲篮球运动员比赛得分更稳定,中位数为26 |
| B、甲篮球运动员比赛得分更稳定,中位数为27 |
| C、乙篮球运动员比赛得分更稳定,中位数为31 |
| D、乙篮球运动员比赛得分更稳定,中位数为36 |
下列各数中最小的一个是( )
| A、111111(2) |
| B、210(6) |
| C、1000(4) |
| D、101(8) |