题目内容
函数f（x）=2sin2x（x∈R）是（ ）
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
考点：正弦函数的奇偶性
专题：三角函数的图像与性质
分析：由条件可得函数f（x）满足定义域关于原点对称，且f（-x）=-f（x），从而格局函数的奇偶性的定义作出判断．
解答：
解：根据函数f（x）=2sin2x（x∈R），可得函数f（x）满足定义域关于原点对称，
且f（-x）=sin（-2x）=-sin2x=-f（x），
故函数为奇函数，
故选：B．
且f（-x）=sin（-2x）=-sin2x=-f（x），
故函数为奇函数，
故选：B．
点评：本题主要考查函数的奇偶性的判断方法，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
设函数f（x）=x2-12x+b，则下列结论正确的是（ ）
| A、函数f（x）在（-∞，-1）上单调递增 |
| B、函数f（x）在（-∞，-1）上单调递减 |
| C、若b=-6，则函数f（x）的图象在点（-2，f（-2））处的切线方程为y=10 |
| D、若b=0，则函数f（x）的图象与直线y=10只有一个公共点 |
两条直线x+2y+1=0与2x-y+1=0的位置关系是（ ）
| A、平行 | B、垂直 |
| C、相交且不垂直 | D、重合 |
已知函数f（x）=sin（
-x）（x∈R），下面结论正确的是（ ）
| π |
| 2 |
A、函数f（x）的最小正周期为
| ||
B、函数f（x）在区间[0，
| ||
| C、函数f（x）是奇函数 | ||
| D、函数f（x）的图象关于直线x=0对称 |
函数y=x3-ax在x=1处的切线与直线x-2y=0垂直，则a的值为（ ）
| A、5 | ||
B、
| ||
| C、3 | ||
D、
|
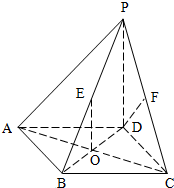已知在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧棱PD⊥平面ABCD，且PD=2，O为底面对角线的交点，E、F分别为棱PB，PC的中点