题目内容
已知函数f（x）=sin（
-x）（x∈R），下面结论正确的是（ ）
| π |
| 2 |
A、函数f（x）的最小正周期为
| ||
B、函数f（x）在区间[0，
| ||
| C、函数f（x）是奇函数 | ||
| D、函数f（x）的图象关于直线x=0对称 |
考点：正弦函数的单调性,正弦函数的奇偶性
专题：三角函数的图像与性质
分析：由条件利用余弦函数的周期新、奇偶性、及其图象的对称性，判断各个选项是否正确，从而得出结论．
解答：
解：∵函数f（x）=sin（
-x）=cosx，∴函数的周期为2π，故排除A；
可得函数f（x）在区间[0，
]上是减函数，故排除B；
可得函数f（x）为偶函数，图象关于y轴（即直线x=0）对称，故排除C，且D满足条件，
故选：D．
| π |
| 2 |
可得函数f（x）在区间[0，
| π |
| 2 |
可得函数f（x）为偶函数，图象关于y轴（即直线x=0）对称，故排除C，且D满足条件，
故选：D．
点评：本题主要考查诱导公式的应用，余弦函数的周期新、奇偶性、及其图象的对称性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
南宁市十二路公共汽车每5分钟一趟，某位同学每天乘十二路公共汽车上学，则他等车时间小于3分钟的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
⊙O1：x2+y2=1与⊙O2：（x-3）2+（y+4）2=9，则⊙O1与⊙O2的位置关系为（ ）
| A、相交 | B、外切 | C、内切 | D、外离 |
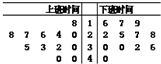某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图如图，则上班、下班时间行驶速度的中位数分别是（ ）| A、28、27.5 |
| B、28、28.5 |
| C、29、27.5 |
| D、29、28.5 |
已知直线l过点P（4，3），圆C：x2+y2=25，则直线l与圆的位置关系是（ ）
| A、相交 | B、相切 |
| C、相交或相切 | D、相离 |
函数f（x）=2sin2x（x∈R）是（ ）
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |