题目内容
正方体ABCD-A′B′C′D′中，异面直线BD与AD′所成的角的大小为 ．
考点：异面直线及其所成的角
专题：空间角
分析：连结B′D′，AB′，BD∥B′D′，∠AD′B′是异面直线BD与AD′所成的角，由△AB′D′是等边三角形，能求出异面直线BD与AD′所成的角．
解答：
解：
连结B′D′，AB′，
∵BD∥B′D′，∴∠AD′B′是异面直线BD与AD′所成的角，
∵△AB′D′是等边三角形，
∴∠AD′B′=60°，
∴异面直线BD与AD′所成的角为60°．
故答案为：60°．
连结B′D′，AB′，∵BD∥B′D′，∴∠AD′B′是异面直线BD与AD′所成的角，
∵△AB′D′是等边三角形，
∴∠AD′B′=60°，
∴异面直线BD与AD′所成的角为60°．
故答案为：60°．
点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
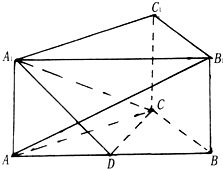如图所示，在直三棱柱ABC-A1B1C1中，AA1=2，AB=4，AC=BC=3，D为AB的中点，且AB1⊥A1C