题目内容
求y=sin（2x+
）在[-
，
]的最值．
| π |
| 3 |
| π |
| 2 |
| π |
| 4 |
考点：三角函数的最值
专题：三角函数的求值
分析：由题意可得2x+
∈[-
，
]，由三角函数的最值可得．
| π |
| 3 |
| 2π |
| 3 |
| 5π |
| 6 |
解答：
解：∵x∈[-
，
]，
∴2x+
∈[-
，
]，
∴当2x+
=-
即x=-
时，y取最小值-1；
当2x+
=
即x=
时，y取最大值1
| π |
| 2 |
| π |
| 4 |
∴2x+
| π |
| 3 |
| 2π |
| 3 |
| 5π |
| 6 |
∴当2x+
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
当2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
点评：本题考查三角函数区间上的最值，属基础题．
练习册系列答案
相关题目
当x∈[1，5]时，函数f（x）=3x2-4x+c的值域为（ ）
| A、[f（1），f（5）] | ||
B、[f（1），f（
| ||
C、[f（
| ||
| D、[c，f（5）] |
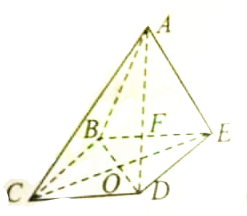如图所示，几何体A-BCDE是底面边长为4的菱形，∠CBE=120°，侧面ABE是等边三角形，BD∩CE=O，F是BE上的动点，面ABE⊥面BCDE；函数y=x2+bx+c在区间[0，+∞）上具有单调性，则实数b应满足的条件是（ ）
| A、b≥0 | B、b≤0 |
| C、b＞0 | D、b＜0 |
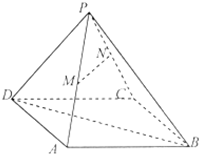如图，已知四棱锥P-ABCD，底面四边形ABCD为菱形，AB=2，BD=2