题目内容
已知双曲线x2-
=1的两个焦点分别为F1、F2,点P为双曲线上一点,且∠F1PF2=90°,则△F1PF2的周长等于( )
| y2 |
| 3 |
| A、6 | ||
| B、8 | ||
C、4+2
| ||
D、2+2
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的a,b,c,运用双曲线的定义,以及完全平方公式,结合勾股定理,即可求得所求的周长.
解答:
解:双曲线x2-
=1的a=1,b=
,c=
=2,
设P为右支上一点,则|PF1|-|PF2|=2a=2,
∠F1PF2=90°,则|PF1|2+|PF2|2=|F1F2|2=4c2=16,
即有(|PF1|-|PF2|)2+2|PF1|•|PF2|=16,
则|PF1|•|PF2|=6,
即(|PF1|+|PF2|)2=|PF1|2+|PF2|2+2|PF1|•|PF2|=16+12=28,
即有|PF1|+|PF2|=2
,
则△F1PF2的周长为|PF1|+|PF2|+|F1F2|=2
+4.
故选C.
| y2 |
| 3 |
| 3 |
| 1+3 |
设P为右支上一点,则|PF1|-|PF2|=2a=2,
∠F1PF2=90°,则|PF1|2+|PF2|2=|F1F2|2=4c2=16,
即有(|PF1|-|PF2|)2+2|PF1|•|PF2|=16,
则|PF1|•|PF2|=6,
即(|PF1|+|PF2|)2=|PF1|2+|PF2|2+2|PF1|•|PF2|=16+12=28,
即有|PF1|+|PF2|=2
| 7 |
则△F1PF2的周长为|PF1|+|PF2|+|F1F2|=2
| 7 |
故选C.
点评:本题考查双曲线的定义、方程和性质,考查化简变形能力和运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=
sinx(
<x<
)的值域是( )
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(0,
| ||||
| D、(0,1) |
下列函数在(0,+∞)上单调递增的是( )
| A、y=(x-1)2 | ||
| B、y=lg(x+3) | ||
| C、y=21-x | ||
D、y=
|
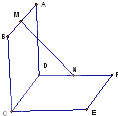 如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点.若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值.
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点.若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值.