题目内容
设函数f(x)=lnx,g(x)=
.
(Ⅰ)求函数y=f(x)-g(x)的单调区间;
(Ⅱ)当x>1时,证明:f(x)>g(x);
(Ⅲ)函数f(x)与f(x)的图象在交点处是否有公切线?若有,求出该公切线的方程;若没有,请说明理由.
| 2(x-1) |
| x+1 |
(Ⅰ)求函数y=f(x)-g(x)的单调区间;
(Ⅱ)当x>1时,证明:f(x)>g(x);
(Ⅲ)函数f(x)与f(x)的图象在交点处是否有公切线?若有,求出该公切线的方程;若没有,请说明理由.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:(Ⅰ)求函数y=f(x)-g(x)定义域并求导,从而判断单调区间;
(Ⅱ)由函数y=f(x)-g(x)在(0,+∞)上是增函数,且当x=1时,y=f(x)-g(x)=0-0=0,从而得证;
(Ⅲ)由(Ⅰ)、(Ⅱ)可得,函数f(x)与g(x)的图象的交点为(1,0),从而求导数,最终求公共切线.
(Ⅱ)由函数y=f(x)-g(x)在(0,+∞)上是增函数,且当x=1时,y=f(x)-g(x)=0-0=0,从而得证;
(Ⅲ)由(Ⅰ)、(Ⅱ)可得,函数f(x)与g(x)的图象的交点为(1,0),从而求导数,最终求公共切线.
解答:
解:(Ⅰ)y=f(x)-g(x)=lnx-
的定义域为(0,+∞),
y′=
-
=
≥0,
故函数y=f(x)-g(x)在(0,+∞)上是增函数;
(Ⅱ)证明:∵函数y=f(x)-g(x)在(0,+∞)上是增函数;
又∵当x=1时,y=f(x)-g(x)=0-0=0,
∴当x>1时,f(x)-g(x)>f(1)-g(1)=0,
∴f(x)>g(x);
(Ⅲ)由(Ⅰ)、(Ⅱ)可得,
函数f(x)与g(x)的图象的交点为(1,0),
在该点处的导数分别为:
f′(1)=1,g′(1)=1;
故在(1,0)处有公切线,
其公共切线为y-0=x-1,
即x-y-1=0.
| 2(x-1) |
| x+1 |
y′=
| 1 |
| x |
| 4 |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
故函数y=f(x)-g(x)在(0,+∞)上是增函数;
(Ⅱ)证明:∵函数y=f(x)-g(x)在(0,+∞)上是增函数;
又∵当x=1时,y=f(x)-g(x)=0-0=0,
∴当x>1时,f(x)-g(x)>f(1)-g(1)=0,
∴f(x)>g(x);
(Ⅲ)由(Ⅰ)、(Ⅱ)可得,
函数f(x)与g(x)的图象的交点为(1,0),
在该点处的导数分别为:
f′(1)=1,g′(1)=1;
故在(1,0)处有公切线,
其公共切线为y-0=x-1,
即x-y-1=0.
点评:本题考查了导数的综合应用,同时考查了导数的几何意义,属于中档题.

练习册系列答案
相关题目
设M是△ABC边BC上任意一点,N为AM上一点且AN=2NM,若
=λ
+μ
,则λ+μ=( )
| AN |
| AB |
| AC |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
3名同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
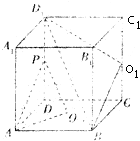 如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证:
如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证: