题目内容
已知函数f(x)=x3-ax-1
(1)若f(x)在(-∞,+∞)上单调递增,求实数a的取值范围;
(2)是否存在实数a,使f(x)在(-1,1)上单调递减?若存在,求出a的取值范围;若不存在试说明理由.
解析 (1)f′(x)=3x2-a
由Δ≤0,即12a≤0,解得a≤0,
因此当f(x)在(-∞,+∞)上单调递增时,a的取值范围是(-∞,0].
(2)若f(x)在(-1,1)上单调递减,
则对于任意x∈(-1,1)不等式f′(x)=3x2-a≤0恒成立
即a≥3x2,又x∈(-1,1),则3x2<3因此a≥3
函数f(x)在(-1,1)上单调递减,实数a的取值范围是[3,+∞).

练习册系列答案
相关题目
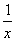 的单调增区间为( ).
的单调增区间为( ).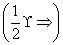

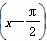 (x∈R),下面结论错误的是( ).
(x∈R),下面结论错误的是( ). 上是增函数
上是增函数