题目内容
设函数f(x)=ax3-3x+1(x∈R),若对于任意x∈[-1,1],都有f(x)≥0成立,则实数a的值为________.
4
解析 (构造法)若x=0,则不论a取何值,f(x)≥0显然成立;
当x>0,即x∈(0,1]时,f(x)=ax3-3x+1≥0可化为a≥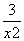 -
-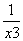 .设g(x)=
.设g(x)=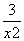 -
-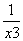 ,则g′(x)=
,则g′(x)=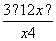 ,
,
所以g(x)在区间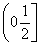 上单调递增,在区间
上单调递增,在区间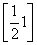 上单调递减,
上单调递减,
因此g(x)max=g =4,从而a≥4.
=4,从而a≥4.
当x<0,即x∈[-1,0)时,同理a≤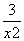 -
-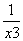 .
.
g(x)在区间[-1,0)上单调递增,
∴g(x)min=g(-1)=4,从而a≤4,综上可知a=4.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

 );
); 
 -aln x(a∈R).
-aln x(a∈R).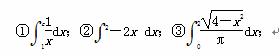 ④
④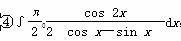 ,积分值等于1的个数是( ).
,积分值等于1的个数是( ).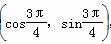 ,则sin β=________,
,则sin β=________,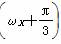 (ω>0)的最小正周期为π,则该函数的图象( )
(ω>0)的最小正周期为π,则该函数的图象( )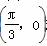 对称 B.关于直线x=
对称 B.关于直线x=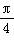 对称
对称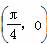 对称 D.关于直线x=
对称 D.关于直线x=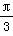 对称
对称