题目内容
设函数f(x)＝x|x|＋bx＋c，给出下列命题：
①b＝0，c>0时，方程f(x)＝0只有一个实数根；
②c＝0时，y＝f(x)是奇函数；
③方程f(x)＝0至多有两个实根．
上述三个命题中所有正确命题的序号为________．
①②解析 ①f(x)＝x|x|＋c＝
，
如图①，曲线与x轴只有一个交点，所以方程f(x)＝0只有一个实数根，正确．
②c＝0时，f(x)＝x|x|＋bx，显然是奇函数．
③当c＝0，b<0时，
f(x)＝x|x|＋bx＝
.
如图②，方程f(x)＝0可以有三个实数根．
综上所述，正确命题的序号为①②.
答案
练习册系列答案
名校课堂系列答案
相关题目
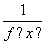，当1≤x≤2时，f(x)＝x－2，则f(6.5)＝( )
的值．
