题目内容
设f0(x)＝sin x，f1(x)＝f′0(x)，f2(x)＝f′1(x)，…，fn＋1(x)＝f′n(x)，n∈N，则f2 013(x)等于( )．
A．sin x B．－sin x C．cos x D．－cos x
C解析 ∵f0(x)＝sin x，f1(x)＝cos x，
f2(x)＝－sin x，f3(x)＝－cos x，f4(x)＝sin x，…
∴fn(x)＝fn＋4(x)，故f2 012(x)＝f0(x)＝sin x，
∴f2 013(x)＝f′2 012(x)＝cos x.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
的值．
)； 
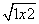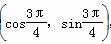，则sin β＝________，