题目内容
已知函数f(x)=x2+(k-3)x+2-k.
(1)证明:函数f(x)至少有一个零点;
(2)对任意k∈[-1,1],f(x)恒大于零,求x的取值范围.
(1)证明:函数f(x)至少有一个零点;
(2)对任意k∈[-1,1],f(x)恒大于零,求x的取值范围.
考点:函数零点的判定定理,二次函数的性质
专题:函数的性质及应用
分析:(1)令f(x)=0,得到判别式大于等于0,从而得到结论;(2)令g(k)=(x-1)k+x2-3x+2,通过讨论x的范围,得到不等式组,解出即可.
解答:
证明:(1)令x2+(k-3)x+2-k=0,
∵△=(k-1)2≥0,
∴函数f(x)至少有一个零点.
(2)令g(k)=(x-1)k+x2-3x+2,
当x=1时,g(k)=0,不满足条件,舍去,
当x≠1时,由题意得
,
即
,
解得:x>3或x<1,
综上所述:满足条件的x的取值范围为:{x|x>3或x<1}.
∵△=(k-1)2≥0,
∴函数f(x)至少有一个零点.
(2)令g(k)=(x-1)k+x2-3x+2,
当x=1时,g(k)=0,不满足条件,舍去,
当x≠1时,由题意得
|
即
|
解得:x>3或x<1,
综上所述:满足条件的x的取值范围为:{x|x>3或x<1}.
点评:本题考查了函数的零点问题,考查了二次函数的性质,是一道基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知集合A={1,2,0,-2},B={0,2,4},则A∩B=( )
| A、{1,-2} |
| B、{0,2} |
| C、{0,1,2,4,-2} |
| D、{1,-2,4} |
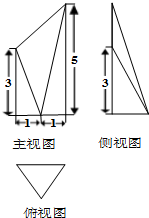 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
已知关于x的不等式
-
>0的解集为(-∞,-2)∪(1,2),则关于x的不等式
-
>0的解集为( )
| x+a |
| x+b |
| x+c |
| x+d |
| alnx-1 |
| blnx-1 |
| clnx-1 |
| dlnx-1 |
A、(-1,-
| ||||||||
B、(
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,
|

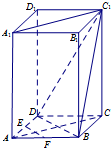 在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.
在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.