题目内容
已知sinx,cosx是方程x2-ax+
=0的两根,且π<α<
,求
的值.
| 1 |
| 2 |
| 3π |
| 2 |
| tan(3π-α)cos(π+α)-cos(-π+α) | ||||
sin(
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:首先利用一元二次方程根和系数的关系,建立关系式求出a的值,进一步对三角函数进行恒等变换,化简求出函数值.
解答:
解:已知sinα,cosα是方程x2-ax+
=0的两根
则:sinα+cosα=a sinαcosα=
利用sin2α+cos2α=1sin2x+cos2x=1
解得:(sinα+cosα)2-2siαcosα=1
求得a2-1=1
所以:a=±
由于:π<α<
a=-
=
=1
| 1 |
| 2 |
则:sinα+cosα=a sinαcosα=
| 1 |
| 2 |
利用sin2α+cos2α=1sin2x+cos2x=1
解得:(sinα+cosα)2-2siαcosα=1
求得a2-1=1
所以:a=±
| 2 |
由于:π<α<
| 3π |
| 2 |
a=-
| 2 |
| tan(3π-α)cos(π+α)-cos(-π+α) | ||||
sin(
|
| (-tanα)(-cosα)+cosα |
| cosα+sinα |
点评:本题考查的知识点:同角三角函数恒等关系式的变换,一元二次方程根和系数的关系,三角函数的诱导公式的应用,求函数的值.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知集合A={1,2,0,-2},B={0,2,4},则A∩B=( )
| A、{1,-2} |
| B、{0,2} |
| C、{0,1,2,4,-2} |
| D、{1,-2,4} |
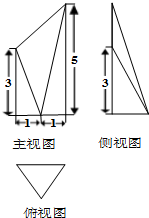 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为( )A、
| ||||
B、
| ||||
C、8
| ||||
D、
|
已知关于x的不等式
-
>0的解集为(-∞,-2)∪(1,2),则关于x的不等式
-
>0的解集为( )
| x+a |
| x+b |
| x+c |
| x+d |
| alnx-1 |
| blnx-1 |
| clnx-1 |
| dlnx-1 |
A、(-1,-
| ||||||||
B、(
| ||||||||
C、(-∞,-
| ||||||||
D、(-∞,
|
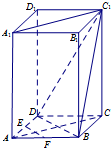 在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.
在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点. 在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别为CC1,C1D1,DD1,CD的中点,N为BC的中点,试在E,F,G,H四个点中找两个点,使这两个点与点N确定一个平面α,且平面α∥平面BB1D1D.