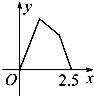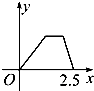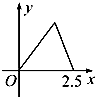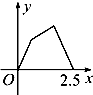题目内容
在等差数列{an}中,a5+a6=16,a8=12,则a3=( )
| A、-4 | B、4 | C、2 | D、-2 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:由题意可得首项和公差的方程组,解方程组代入通项公式可得.
解答:
解:设等差数列{an}的公差为d,
则a5+a6=2a1+9d=16,a8=a1+7d=12,
联立解得a1=
,d=
,
∴a3=
+2×
=4
故选:B
则a5+a6=2a1+9d=16,a8=a1+7d=12,
联立解得a1=
| 4 |
| 5 |
| 8 |
| 5 |
∴a3=
| 4 |
| 5 |
| 8 |
| 5 |
故选:B
点评:本题考查等差数列的通项公式,属基础题.

练习册系列答案
相关题目
复数z=1+i,则
+z=( )
| 1 |
| z |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数y=f(x),x∈[a,b]的图象与直线x=2的交点的个数为( )
| A、1 | B、0 | C、1或0 | D、1或2 |
如图,阴影部分表示的集合是( )


| A、B∩[∁U (A∪C)] |
| B、(A∪B)∪(B∪C) |
| C、(A∪C)∩(∁UB) |
| D、[∁U (A∩C)]∪B |
数列{an}中,已知a1,a2=2,an+2=an+1-an(n∈N*),则a2011=( )
| A、1 | B、-1 | C、-2 | D、2 |
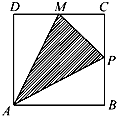 如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )
如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )