题目内容
16.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的体积为( )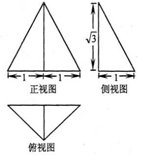
| A. | $\frac{\sqrt{3}}{3}$π | B. | π | C. | $\frac{26}{3}$π | D. | $\frac{32\sqrt{3}}{27}$π |
分析 设外接球半径为r,则有${({\sqrt{3}-r})^2}+1={r^2}$,解出利用体积计算公式即可得出.
解答 解:设外接球半径为r,则有${({\sqrt{3}-r})^2}+1={r^2}$,
所以$r=\frac{{2\sqrt{3}}}{3}$,所以$V=\frac{4}{3}π{r^3}=\frac{{32\sqrt{3}}}{27}π$.
故选:D.
点评 本题考查了三棱锥的三视图、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知f(x)满足f′(2)=3,则$\underset{lim}{{x}_{0}→0}$$\frac{f(2+{2x}_{0})-f(2)}{{x}_{0}}$=( )
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | 6 |
7.已知扇形的圆心角为$\frac{π}{3}$,半径为2,则扇形的弧长为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $4+\frac{2π}{3}$ |
4.执行如图所示的程序框图,输出S值为( )
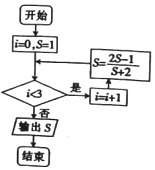

| A. | $-\frac{31}{15}$ | B. | $-\frac{7}{5}$ | C. | $-\frac{31}{17}$ | D. | $-\frac{9}{13}$ |
11.与球心距离为1的截球平面,所得的截面圆的面积为2π,则球的体积为( )
| A. | 8$\sqrt{3}$π | B. | 4$\sqrt{3}$π | C. | 4π | D. | 8π |
8.若cosθ<0,且sin2θ<0,则角θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.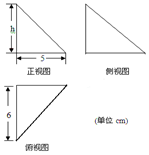 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
 如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )| A. | 55π | B. | 75π | C. | 77π | D. | 65π |