ΧβΡΩΡΎ»ί
‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“―÷ΣMΘ®0Θ§
Θ©Θ§NΘ®0Θ§-
Θ©Θ§ΤΫΟφ…œ“ΜΕ·ΒψP¬ζΉψ|PM|+|PN|=4Θ§Φ«ΒψPΒΡΙλΦΘΈΣPΘ°
Θ®1Θ©«σΙλΦΘPΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…ηΙΐΒψEΘ®0Θ§1Θ©«“≤Μ¥Ι÷±”ΎΉχ±ξ÷αΒΡ÷±œΏl1ΘΚy=kx+b1”κΙλΦΘPœύΫΜ”ΎAΘ§BΝΫΒψΘ§»τy÷α…œ¥φ‘Ύ“ΜΒψQΘ§ ΙΒΟ÷±œΏQAΘ§QBΙΊ”Ύy÷αΕ‘≥ΤΘ§«σ≥ωΒψQΒΡΉχ±ξΘΜ
Θ®3Θ© «Ζώ¥φ‘Ύ≤ΜΙΐΒψEΘ®0Θ§1Θ©Θ§«“≤Μ¥Ι÷±Ήχ±ξ÷αΒΡ÷±œΏlΘ§Υϋ”κΙλΦΘPΦΑ‘≤EΘΚx2+Θ®y-1Θ©2=9¥”ΉσΒΫ”““ά¥ΈΫΜ”ΎCΘ§DΘ§FΘ§GΥΡΒψΘ§«“¬ζΉψ
-
=
-
ΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒ±ΓςOCGΒΡΟφΜΐS»ΓΒΟΉν–Γ÷Β ±k2ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
| 3 |
| 3 |
Θ®1Θ©«σΙλΦΘPΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…ηΙΐΒψEΘ®0Θ§1Θ©«“≤Μ¥Ι÷±”ΎΉχ±ξ÷αΒΡ÷±œΏl1ΘΚy=kx+b1”κΙλΦΘPœύΫΜ”ΎAΘ§BΝΫΒψΘ§»τy÷α…œ¥φ‘Ύ“ΜΒψQΘ§ ΙΒΟ÷±œΏQAΘ§QBΙΊ”Ύy÷αΕ‘≥ΤΘ§«σ≥ωΒψQΒΡΉχ±ξΘΜ
Θ®3Θ© «Ζώ¥φ‘Ύ≤ΜΙΐΒψEΘ®0Θ§1Θ©Θ§«“≤Μ¥Ι÷±Ήχ±ξ÷αΒΡ÷±œΏlΘ§Υϋ”κΙλΦΘPΦΑ‘≤EΘΚx2+Θ®y-1Θ©2=9¥”ΉσΒΫ”““ά¥ΈΫΜ”ΎCΘ§DΘ§FΘ§GΥΡΒψΘ§«“¬ζΉψ
. |
| ED |
. |
| EC |
. |
| EG |
. |
| EF |
ΩΦΒψΘΚ÷±œΏ”κ‘≤ΉΕ«ζœΏΒΡΉέΚœΈ Χβ
Ή®ΧβΘΚ‘≤ΉΕ«ζœΏ÷–ΒΡΉν÷Β”κΖΕΈßΈ Χβ
Ζ÷ΈωΘΚΘ®1Θ©”…“―÷ΣΧθΦΰΆΤΒΦ≥ωΒψPΒΡΙλΦΘ «“‘MΘ§NΈΣΫΙΒψΘ§≥Λ÷α≥ΛΈΣ4Θ§ΫΙΨύΈΣ2
ΒΡΆ÷‘≤Θ§”…¥ΥΡή«σ≥ωΙλΦΘPΒΡΖΫ≥ΧΘ°
Θ®2Θ©…ηΒψQΘ®0Θ§tΘ©Θ§÷±œΏl1ΘΚy=kx+1Θ§”…
Θ§ΒΟΘ®k 12+4Θ©x2+2k1x-3=0Θ§”…¥Υάϊ”ΟΗυΒΡ≈–±π ΫΓΔΈΛ¥οΕ®άμΓΔ÷±œΏΖΫ≥ΧΓΔ–±¬ ΙΪ ΫΡή«σ≥ωΒψQΒΡΉχ±ξΘ°
Θ®3Θ©ΦΌ…η¥φ‘ΎΖϊΚœΧβ“βΒΡ÷±œΏlΘ§…ηΤδΖΫ≥ΧΈΣy=kx+bΘ§«“kΓΌ0Θ§…ηœΏΕΈDFΒΡ÷–ΒψΈΣHΘ§”…
Θ§ΒΟΘ®k2+4Θ©x2+2kbx+b2-4=0Θ§άϊ”ΟΗυΒΡ≈–±π ΫΓΔΈΛ¥οΕ®άμΓΔœρΝΩΓΔΙΙ‘λΖ®¥ΙΨΕΕ®άμΒ»÷Σ Ε’ΦΡή«σ≥ωΓςOCGΒΡΟφΜΐS»ΓΒΟΉν–Γ÷Β ±k2ΒΡ÷ΒΘ°
| 3 |
Θ®2Θ©…ηΒψQΘ®0Θ§tΘ©Θ§÷±œΏl1ΘΚy=kx+1Θ§”…
|
Θ®3Θ©ΦΌ…η¥φ‘ΎΖϊΚœΧβ“βΒΡ÷±œΏlΘ§…ηΤδΖΫ≥ΧΈΣy=kx+bΘ§«“kΓΌ0Θ§…ηœΏΕΈDFΒΡ÷–ΒψΈΣHΘ§”…
|
Ϋβ¥πΘΚ
ΫβΘΚΘ®1Θ©ΓΏ|PM|+|PN|=4ΘΨ2
Θ§
ΓύΒψPΒΡΙλΦΘ «“‘MΘ§NΈΣΫΙΒψΘ§
≥Λ÷α≥ΛΈΣ4Θ§ΫΙΨύΈΣ2
ΒΡΆ÷‘≤Θ§
Φ¥a=2Θ§c=
Θ§Γύb2=a2-c2=1Θ§
ΓύΙλΦΘPΒΡΖΫ≥ΧΈΣ
+x2=1Θ°
Θ®2Θ©…ηΒψQΘ®0Θ§tΘ©Θ§
ΓΏΙΐΒψEΘ®0Θ§1Θ©«“≤Μ¥Ι÷±”ΎΉχ±ξ÷αΒΡ÷±œΏl1ΘΚy=kx+b1”κΙλΦΘPœύΫΜ”ΎAΘ§BΝΫΒψΘ§
Γύb1=1Θ§Γύ÷±œΏl1ΘΚy=k1x+1Θ§
”…
Θ§œϊ»ΞyΘ§ΒΟΘ®k 12+4Θ©x2+2k1x-3=0Θ§
…ηAΘ®x1Θ§y1Θ©Θ§BΘ®
Θ§y2Θ©Θ§
‘ρ
Θ§
ΓύAΘ®x1Θ§k1x1+1Θ©Θ§BΘ®x2Θ§k1x2+1Θ©Θ§
ΓύkAQ=
Θ§kBQ=
Θ§
ΓΏ÷±œΏQAΘ§QBΙΊ”Ύy÷αΕ‘≥ΤΘ§ΓύkAQ+kBQ=
+
=0Θ§
Γύ2k1x1x2+Θ®1-tΘ©Θ®x1+x2Θ©=0Θ§
Γύ2k1Θ®-3Θ©+Θ®1-tΘ©Θ®-2k1Θ©=2k1t-8k1=2Θ®t-4Θ©k1=0Θ§
ΫβΒΟt=4Θ§ΓύQΒψΉχ±ξΘ®0Θ§4Θ©Θ°
Θ®3Θ©ΦΌ…η¥φ‘ΎΖϊΚœΧβ“βΒΡ÷±œΏlΘ§…ηΤδΖΫ≥ΧΈΣy=kx+bΘ§«“kΓΌ0Θ§
…ηœΏΕΈDFΒΡ÷–ΒψΈΣHΘ§
ΓΏ
-
=
-
Θ§
Γύ
+
=
+
=2
Θ§
”…
Θ§œϊ»ΞyΘ§ΒΟΘ®k2+4Θ©x2+2kbx+b2-4=0Θ§
…ηDΘ®x3Θ§y3Θ©Θ§FΘ®x4Θ§y4Θ©Θ§
‘ρ
Θ§
ΓύHΘ®
Θ§
Θ©Θ§
”…kEH=
=-
Θ§ΫβΒΟk2+4=3bΘ§ΓύHΘ®
Θ§
Θ©Θ§
¥ζ»κ≈–±π ΫΘ§ΒΟ0ΘΦk2ΘΦ5Θ§
Γύ¥φ‘Ύ’β―υΒΡ÷±œΏlΖϊΚœΧβ“βΘ§
|EH|=
=
Θ§
”…¥ΙΨΕΕ®άμΘ§ΒΟ|CG|=2
=
Θ§
Ήχ±ξ‘≠ΒψOΒΫ÷±œΏlΒΡΨύάκd=
=
Θ§
ΓύS=
|CG|•d=
ΓΝ
ΓΝ
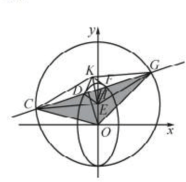
=
(k2+4)
Θ§
ΓύS2=
(k2+4)2•
Θ§
Ννk2+1=rΘ§rΓ Θ®1Θ§6Θ©Θ§
ΙΙ‘λΚ· ΐF(r)=
(r+3)2
Θ§rΓ Θ®1Θ§6Θ©Θ§
FΓδ(r)=
(r+3)
Θ§rΓ Θ®1Θ§6Θ©Θ§
ΝνGΘ®rΘ©=-2r2+81r-243Θ§rΓ Θ®1Θ§6Θ©Θ§
GΘ®rΘ©=-2r+81r-243=0Θ§
Γύr1=
Θ§Μρr2=
Θ®…αΘ©
”÷ΓΏ7ΘΦ
ΘΦ8Θ§Γύ
ΘΦr1=
ΘΦ
Θ§
”÷Β±rΓ Θ®r1Θ§6Θ© ±Θ§GΘ®rΘ©ΘΨ0Θ§
ΓύFΓδΘ®rΘ©ΘΨ0Θ§ΓύFΘ®rΘ©‘ΎΘ®r1 Θ§6Θ©…œΒΞΒςΒί‘ωΘ§
ΓύΒ±k2+1=
Θ§Φ¥k2=
±Θ§
ΓςOCGΒΡΟφΜΐS»ΓΒΟΉν–Γ÷ΒΘ°
| 3 |
ΓύΒψPΒΡΙλΦΘ «“‘MΘ§NΈΣΫΙΒψΘ§
≥Λ÷α≥ΛΈΣ4Θ§ΫΙΨύΈΣ2
| 3 |
Φ¥a=2Θ§c=
| 3 |
ΓύΙλΦΘPΒΡΖΫ≥ΧΈΣ
| y2 |
| 4 |
Θ®2Θ©…ηΒψQΘ®0Θ§tΘ©Θ§
ΓΏΙΐΒψEΘ®0Θ§1Θ©«“≤Μ¥Ι÷±”ΎΉχ±ξ÷αΒΡ÷±œΏl1ΘΚy=kx+b1”κΙλΦΘPœύΫΜ”ΎAΘ§BΝΫΒψΘ§
Γύb1=1Θ§Γύ÷±œΏl1ΘΚy=k1x+1Θ§
”…
|
…ηAΘ®x1Θ§y1Θ©Θ§BΘ®
| x | 2 |
‘ρ
|
ΓύAΘ®x1Θ§k1x1+1Θ©Θ§BΘ®x2Θ§k1x2+1Θ©Θ§
ΓύkAQ=
| k1x1+1-t |
| x1 |
| k1x2+1-t |
| x2 |
ΓΏ÷±œΏQAΘ§QBΙΊ”Ύy÷αΕ‘≥ΤΘ§ΓύkAQ+kBQ=
| k1x1+1-t |
| x1 |
| k1x2+1-t |
| x2 |
Γύ2k1x1x2+Θ®1-tΘ©Θ®x1+x2Θ©=0Θ§
Γύ2k1Θ®-3Θ©+Θ®1-tΘ©Θ®-2k1Θ©=2k1t-8k1=2Θ®t-4Θ©k1=0Θ§
ΫβΒΟt=4Θ§ΓύQΒψΉχ±ξΘ®0Θ§4Θ©Θ°
Θ®3Θ©ΦΌ…η¥φ‘ΎΖϊΚœΧβ“βΒΡ÷±œΏlΘ§…ηΤδΖΫ≥ΧΈΣy=kx+bΘ§«“kΓΌ0Θ§
…ηœΏΕΈDFΒΡ÷–ΒψΈΣHΘ§
ΓΏ
| ED |
| EC |
| EG |
| EF |
Γύ
| ED |
| EF |
| EC |
| EG |
| EH |
”…
|
…ηDΘ®x3Θ§y3Θ©Θ§FΘ®x4Θ§y4Θ©Θ§
‘ρ
|
ΓύHΘ®
| -kb |
| k2+4 |
| 4b |
| k2+4 |
”…kEH=
| ||
|
| 1 |
| k |
| -k |
| 3 |
| 4 |
| 3 |
¥ζ»κ≈–±π ΫΘ§ΒΟ0ΘΦk2ΘΦ5Θ§
Γύ¥φ‘Ύ’β―υΒΡ÷±œΏlΖϊΚœΧβ“βΘ§
|EH|=
(
|
|
”…¥ΙΨΕΕ®άμΘ§ΒΟ|CG|=2
| 9-|EH|2 |
| 2 |
| 3 |
| 80-k2 |
Ήχ±ξ‘≠ΒψOΒΫ÷±œΏlΒΡΨύάκd=
| |b| | ||
|
| k2+4 | ||
3
|
ΓύS=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 80-k2 |
| k2+4 | ||
3
|

=
| 1 |
| 9 |
| ||
|
ΓύS2=
| 1 |
| 81 |
| 80-k2 |
| k2+1 |
Ννk2+1=rΘ§rΓ Θ®1Θ§6Θ©Θ§
ΙΙ‘λΚ· ΐF(r)=
| 1 |
| 81 |
| (81-r) |
| r |
FΓδ(r)=
| 1 |
| 81 |
| (-2r2+81r-243) |
| r2 |
ΝνGΘ®rΘ©=-2r2+81r-243Θ§rΓ Θ®1Θ§6Θ©Θ§
GΘ®rΘ©=-2r+81r-243=0Θ§
Γύr1=
81-9
| ||
| 4 |
81+9
| ||
| 4 |
”÷ΓΏ7ΘΦ
| 57 |
| 9 |
| 4 |
81-9
| ||
| 4 |
| 9 |
| 2 |
”÷Β±rΓ Θ®r1Θ§6Θ© ±Θ§GΘ®rΘ©ΘΨ0Θ§
ΓύFΓδΘ®rΘ©ΘΨ0Θ§ΓύFΘ®rΘ©‘ΎΘ®r1 Θ§6Θ©…œΒΞΒςΒί‘ωΘ§
ΓύΒ±k2+1=
81-9
| ||
| 4 |
77-9
| ||
| 4 |
ΓςOCGΒΡΟφΜΐS»ΓΒΟΉν–Γ÷ΒΘ°
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΆ÷‘≤ΖΫ≥ΧΒΡ«σΖ®Θ§ΩΦ≤ιΒψΒΡΉχ±ξΒΡ«σΖ®Θ§ΩΦ≤ι»ΐΫ«–ΈΟφΜΐ»ΓΉν–Γ÷Β ±≤Έ ΐ÷ΒΒΡ«σΖ®Θ§ΉέΚœ–‘÷ «ΩΘ§Ρ―Ε»¥σΘ§ΫβΧβ ±“Σ»œ’φ…σΧβΘ§±ήΟβ≥ωœ÷‘ΥΥψ…œΒΡ¥μΈσΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
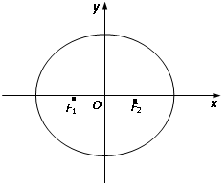 »γΆΦΥυ ΨΘ§“―÷ΣΆ÷‘≤CΒΡΝΫΗωΫΙΒψΖ÷±πΈΣF1Θ®-1Θ§0Θ©ΓΔF2Θ®1Θ§0Θ©Θ§«“F2ΒΫ÷±œΏx-
»γΆΦΥυ ΨΘ§“―÷ΣΆ÷‘≤CΒΡΝΫΗωΫΙΒψΖ÷±πΈΣF1Θ®-1Θ§0Θ©ΓΔF2Θ®1Θ§0Θ©Θ§«“F2ΒΫ÷±œΏx-