题目内容
2.在△ABC中,角A,B,C所对的边分别为a,b,c,若2cos2B=4cosB-3(Ⅰ)求角B的大小
(Ⅱ)若S△ABC=$\sqrt{3}$,asinA+csinC=5sinB,求边b.
分析 (Ⅰ)根据二倍角公式求出cosB的值,即可得出角B的大小;
(Ⅱ)由三角形面积公式以及正弦、余弦定理,即可求出边b的大小.
解答 解:(Ⅰ)△ABC中,2cos2B=4cosB-3,
∴2(2cos2B-1)=4cosB-3,
即4cos2B-4cosB+1=0,
解得cosB=$\frac{1}{2}$;
又B∈[0,π],
∴B=$\frac{π}{3}$;
(Ⅱ)由面积公式得S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$acsin$\frac{π}{3}$=$\sqrt{3}$,
解得ac=4,
又asinA+csinC=5sinB,
∴a2+c2=5b,
由余弦定理得,
b2=a2+c2-2accosB=5b-2×4×$\frac{1}{2}$=5b-4,
∴b2-5b+4=0,
解得b=1或b=4;
又a2+c2=5b≥2ac=8,
∴b≥$\frac{8}{5}$,
故b=4.
点评 本题考查了三角恒等变换以及正弦、余弦定理的应用问题,是综合性题目.

练习册系列答案
相关题目
9.已知一个水平放置的正方形用斜二测画法作出的直观图是一个平行四边形,若平行四边形中有一条边为4,则此正方形的面积是( )
| A. | .16或36 | B. | 36或64 | C. | 16或64 | D. | 36 |
13.若等差数列{an}的公差为d,前n项和为Sn,记bn=$\frac{{S}_{n}}{n}$,则( )
| A. | 数列{bn}是等差数列,{bn}的公差也为d | |
| B. | 数列{bn}是等差数列,{bn}的公差为2d | |
| C. | 数列{an+bn}是等差数列,{an+bn}的公差为d | |
| D. | 数列{an-bn}是等差数列,{an-bn}的公差为$\frac{d}{2}$ |
10.$\int_{0}^{π}{({cosx+1})}dx$等于( )
| A. | 1 | B. | 0 | C. | π | D. | π+1 |
17.双曲线x2-$\frac{{y}^{2}}{4}$=1的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
7.已知f(x)=5x5+4x4+3x3+2x2+x+1,若用秦九韶算法求f(5)的值,下面说法正确的是( )
| A. | 至多4乘法运算和5次加法运算 | B. | 15次乘法运算和5次加法运算 | ||
| C. | 10次乘法运算和5次加法运算 | D. | 至多5次乘法运算和5次加法运算 |
14.执行如图所示的程序框图,若输入x=2,则输出y的值为( )
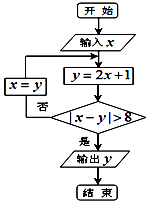

| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
11.若a∈R,则“a>0”是“a+$\frac{1}{a}$≥2”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |