若集合A={-1.0.1.2}.B={x|x+1＞0}.则A∩B={0.1.2}．题目和参考答案——青夏教育精英家教网——

题目内容

12．若集合A={-1，0，1，2}，B={x|x+1＞0}，则A∩B={0，1，2}．

分析先分别求出集合A，B，由此利用交集定义能求出A∩B．

解答解：∵集合A={-1，0，1，2}，
B={x|x+1＞0}={x|x＞-1}，
∴A∩B={0，1，2}．
故答案为：{0，1，2}．

点评本题考查交集的求法，是基础题，解题时要认真审题，注意交集性质的合理运用．

练习册系列答案

聚焦小考冲刺48天系列答案

聚焦新中考系列答案

鸿翔教育决胜中考系列答案

绝对名师系列答案

开心教程系列答案

开心15天精彩寒假巧计划江苏凤凰科学技术出版社系列答案

考出好成绩系列答案

考能大提升系列答案

考前一搏系列答案

考易通初中全程复习导航系列答案

相关题目

2．在△ABC中，角A，B，C所对的边分别为a，b，c，若2cos2B=4cosB-3
（Ⅰ）求角B的大小
（Ⅱ）若S_△ABC=$\sqrt{3}$，asinA+csinC=5sinB，求边b．

3．若函数f（x）满足对于任意实数a，b，c，都有f（a），f（b），f（c）为某三角形的三边长，则成f（x）为“可构造三角形函数”，已知f（x）=$\frac{{2}^{x}-t}{{2}^{x}+1}$是“可构造三角形函数”，则实数t的取值范围是（　　）

[-2，-$\frac{1}{2}$]

20．若$\overrightarrow{a}$=（1，λ，2），$\overrightarrow{b}$=（2，-1，2），$\overrightarrow{c}$=（1，4，4），且$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$共面，则λ=（　　）

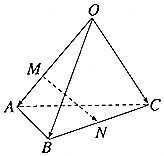如图，四面体OABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，点M在OA上，且OM=2MA，N为BC的中点，$\overrightarrow{MN}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$，则x+y+z=$\frac{1}{3}$．

17．若a=log₃2，b=2^0.3，c=log${\;}_{\frac{1}{5}}$2，则a，b，c的大小关系用“＜”表示为c＜a＜b．

如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．
（1）求|$\overrightarrow{AB}$|；
（2）已知点D是AB上一点，满足$\overrightarrow{AD}$=λ$\overrightarrow{AB}$，点E是边CB上一点，满足$\overrightarrow{BE}$=λ$\overrightarrow{BC}$．
①当λ=$\frac{1}{2}$时，求$\overrightarrow{AE}$•$\overrightarrow{CD}$；
②是否存在非零实数λ，使得$\overrightarrow{AE}$⊥$\overrightarrow{CD}$？若存在，求出的λ值；若不存在，请说明理由．

1．执行如图程序中，若输出y的值为1，则输入x的值为（　　）

2．已知直线l：kx+y-3=0与圆x²+y²=3交于两点A，B且△OAB为等边三角形（O为坐标原点），则k=（　　）