题目内容

14．执行如图所示的程序框图，若输入x=2，则输出y的值为（　　）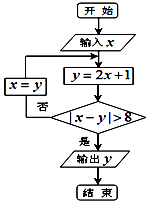
A．5B．11C．23D．47

分析 分析程序框图，循环体为“直到型”循环结构，按照循环结构进行运算，即可求出满足题意的y值．

解答 解：根据题意，本程序框图为求y的和
循环体为“直到型”循环结构，输入x=2，
第一次循环：y=2×2+1=5，|x-y|=3≤8，x=5；
第二次循环：y=2×5+1=11，|x-y|=6≤8，x=11；
第三次循环：y=2×11+1=23，
∵|x-y|=12＞8，
∴结束循环，输出y=23．
故选：C．

点评 本题为程序框图题，考查对循环结构的理解和认识，按照循环结构运算后得出结果．属于基础题．

练习册系列答案
相关题目
1．已知函数f（x）=ex-ax，（e为自然对数的底数）．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若对任意实数x恒有f（x）≥0，求实数a的取值范围．
5．已知函数$f（x）=1-2{sin^2}（x+\frac{π}{8}）+2sin（x+\frac{π}{8}）cos（x+\frac{π}{8}）$．
（1）求f（x）的最小正周期及单调增区间；
（2）求f（x）在区间$[{-\frac{π}{4}，\frac{3π}{8}}]$上的最值．
2．在△ABC中，角A，B，C所对的边分别为a，b，c，若2cos2B=4cosB-3
（Ⅰ）求角B的大小
（Ⅱ）若S△ABC=$\sqrt{3}$，asinA+csinC=5sinB，求边b．
9．设fn（x）是等比数列1，-x，x2，…，（-x）n的各项和，则f2016（2）等于（　　）
A．$\frac{{{2^{2016}}+1}}{3}$B．$\frac{{{2^{2016}}-1}}{3}$C．$\frac{{{2^{2017}}+1}}{3}$D．$\frac{{{2^{2017}}-1}}{3}$
19．已知各项均为正数的等比数列{an}中，$3{a_1}，\frac{1}{2}{a_3}，2{a_2}$成等差数列，则$\frac{{{a_{11}}+{a_{13}}}}{{{a_8}+{a_{10}}}}$=（　　）
A．27B．-1或27C．3D．-1或3
6．已知命题p：不等式x2-2ax-2a+3≥0恒成立；命题q：不等式x2+ax+2＜0有解．
（Ⅰ）若p∨q和￢q均为真命题，求实数a的取值范围；
（Ⅱ）若p是真命题，抛物线y=x2与直线y=ax+1相交于M，N两点，O为坐标原点，求△OMN面积的最大值．
3．若函数f（x）满足对于任意实数a，b，c，都有f（a），f（b），f（c）为某三角形的三边长，则成f（x）为“可构造三角形函数”，已知f（x）=$\frac{{2}^{x}-t}{{2}^{x}+1}$是“可构造三角形函数”，则实数t的取值范围是（　　）
A．[-1，0]B．（-∞，0]C．[-2，-1]D．[-2，-$\frac{1}{2}$]
4．如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．
（1）求|$\overrightarrow{AB}$|；
（2）已知点D是AB上一点，满足$\overrightarrow{AD}$=λ$\overrightarrow{AB}$，点E是边CB上一点，满足$\overrightarrow{BE}$=λ$\overrightarrow{BC}$．
①当λ=$\frac{1}{2}$时，求$\overrightarrow{AE}$•$\overrightarrow{CD}$；
②是否存在非零实数λ，使得$\overrightarrow{AE}$⊥$\overrightarrow{CD}$？若存在，求出的λ值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网