题目内容
6．实验测得五组（x，y）的值是（1，2）（2，4）（3，4）（4，7）（5，8），若线性回归方程为$\stackrel{∧}{y}$=0.7x+$\stackrel{∧}{a}$，则$\stackrel{∧}{a}$的值是（ ）| A． | 1.4 | B． | 1.9 | C． | 2.2 | D． | 2.9 |
分析 根据五组（x，y）的值计算$\overline{x}$、$\overline{y}$，利用线性回归方程过样本中心点求出$\stackrel{∧}{a}$的值．
解答 解：根据五组（x，y）的值，计算
$\overline{x}$=$\frac{1}{5}$×（1+2+3+4+5）=3，
$\overline{y}$=$\frac{1}{5}$×（2+4+4+7+8）=5，
且线性回归方程$\stackrel{∧}{y}$=0.7x+$\stackrel{∧}{a}$过样本中心点，
则$\stackrel{∧}{a}$=$\overline{y}$-0.7$\overline{x}$=5-0.7×3=2.9．
故选：D．
点评 本题考查了平均数与线性回归方程过样本中心点的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
18．过双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F作x轴的垂线，交双曲线C于M，N两点，A为左顶点，设∠MAN=θ，双曲线C的离心率为f（θ），则f（$\frac{2π}{3}$）-f（$\frac{π}{3}$）等于（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
1．
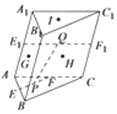如图，在三棱柱ABC-A1B1C1中，E，F，E1，F1分别为棱AB，AC，AA1，CC1的中点，点G，H分别为四边形ABB1A1，BCC1B1对角线的交点，点I为△A1B1C1的外心，P，Q分别在直线EF，E1F1上运动，则在G，H，I，这三个点中，动直线PQ（ ）
如图，在三棱柱ABC-A1B1C1中，E，F，E1，F1分别为棱AB，AC，AA1，CC1的中点，点G，H分别为四边形ABB1A1，BCC1B1对角线的交点，点I为△A1B1C1的外心，P，Q分别在直线EF，E1F1上运动，则在G，H，I，这三个点中，动直线PQ（ ）| A． | 只可能经过点I | B． | 只可能经过点G，H | ||
| C． | 可能经过点G，H，I | D． | 不可能经过点G，H，I |
10．已知一个算法的程序框图如图所示，当输出的结果为$\frac{1}{2}$时，则输入的x值为（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | -1或$\sqrt{2}$ | D． | -1或$\sqrt{10}$ |
某公司2017年元旦晚会现场，为了活跃气氛，将在晚会节目表演过程中进行抽奖活动．
，则
的值是 （ ）
B．9 C．
D．