题目内容
17.已知两定点A(-2,0),B(1,0),若圆心在直线x-y-1=0上且半径为1的动圆P上存在一点Q满足|QA|=2|QB|,则点P横坐标a的取值范围为$\frac{3-\sqrt{17}}{2}≤a≤1$或2≤a≤$\frac{3+\sqrt{17}}{2}$.分析 求出点Q的轨迹为圆,Q在圆P上,也在圆(x-2)2+y2=4上,所以两圆有公共点,即可得出结论.
解答 解:设Q点的坐标为(x,y),则(x+2)2+y2=4[(x-1)2+y2],即(x-2)2+y2=4,所以点Q的轨迹为圆,
而P在直线x-y-1=0上,所以P(a,a-1),所以圆P的方程为(x-a)2+(y-a+1)2=1,
而Q在圆P上,也在圆(x-2)2+y2=4上,所以两圆有公共点,所以2-1≤$\sqrt{(a-2)^{2}+(a-1)^{2}}$≤2+1,
从而解得$\frac{3-\sqrt{17}}{2}≤a≤1$或2≤a≤$\frac{3+\sqrt{17}}{2}$,
故a的范围为:$\frac{3-\sqrt{17}}{2}≤a≤1$或2≤a≤$\frac{3+\sqrt{17}}{2}$.
故答案为$\frac{3-\sqrt{17}}{2}≤a≤1$或2≤a≤$\frac{3+\sqrt{17}}{2}$.
点评 本题考查轨迹方程,考查圆与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
前不久商丘市因环境污染严重被环保部约谈后,商丘市近期加大环境治理力度,下表提供了商丘某企业节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程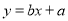 ;
;
(Ⅱ)已知该企业技改前100吨甲产品的生产能耗为90吨标准煤,试根据(Ⅰ)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)参考公式: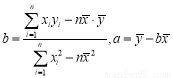
9.已知全集U={1,2,3},集合A={1},B={2},则∁U(A∪B)=( )
| A. | ∅ | B. | U | C. | {1,2} | D. | {3} |
6.已知复数z=$\frac{1+ai}{1-i}$(a∈R)的虚部为1,则a=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |