��Ŀ����
17�� ij��˾2017��Ԫ�������ֳ���Ϊ�˻�Ծ���գ����������Ŀ���ݹ����н��г齱���
ij��˾2017��Ԫ�������ֳ���Ϊ�˻�Ծ���գ����������Ŀ���ݹ����н��г齱�����1������Ҫ�ӵ�һ�ž�����6λ�α�A��B��C��D��E��F�������ȡ2����̨�齱����α�A�ͼα�B������һ����̨�齱�ĸ��ʣ�
��2���齱��Ĺ����ǣ��α�ͨ����������ʹ�����Զ���������[0��1]֮��������x��y��������ͼ��ʾ�ij����ͼִ�У���������ʾ���н�������üα��н�����������ʾ��лл�������н�����üα��н��ĸ��ʣ�
���� ��1�����ݹŵ���͵ĸ��ʹ�ʽ���ɵ�A��B������һ����̨�齱�ĸ��ʣ�
��2��ȷ������0��x��1��0��y��1�������������$\left\{\begin{array}{l}{\stackrel{2x-y-1��0}{0��x��1}}\\{0��y��1}\end{array}\right.$����������Ϊͼ�е���Ӱ���֣��������������ô����н��ĸ��ʣ�
��� �⣺��1��6λ�α������г�ȡ2����̨�齱�Ļ����¼��У�a��b������a��c������a��d������a��e������a��f������b��c������b��d������b��e������b��f������c��d������c��e������c��f������d��e������d��f������e��f����15�֣�����a��b������һ����̨�齱�Ļ����¼���9�֣�
��a��b������һ����̨�齱�ĸ���Ϊ$\frac{9}{15}$=$\frac{3}{5}$��
��2������֪0��x��1��0��y��1���㣨x��y������ͼ��ʾ��������OABC�ڣ�
������$\left\{\begin{array}{l}{\stackrel{2x-y-1��0}{0��x��1}}\\{0��y��1}\end{array}\right.$���õ�������Ϊͼ�е���Ӱ���֣�
��2x-y-1=0����y=0���ɵ�x=$\frac{1}{2}$����y=1���ɵ�x=1��
����x��y��[0��1]ʱ����2x-y-1��0����������ΪS��=$\frac{1}{2}��$��1+$\frac{1}{2}$����1=$\frac{3}{4}$��
��ô����н��ĸ���Ϊ$\frac{\frac{3}{4}}{1}$=$\frac{3}{4}$��
���� ���⿼�������ͳ��֪ʶ������ֲ������������ʵļ��㣬ȷ�����ʵ������ǹؼ������ڻ����⣮

 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�| A�� | ∅ | B�� | U | C�� | {1��2} | D�� | {3} |
| A�� | 2016 | B�� | -2016 | C�� | 3024 | D�� | -3024 |
| A�� | 1.4 | B�� | 1.9 | C�� | 2.2 | D�� | 2.9 |
| A�� | 1.2 | B�� | 1.3 | C�� | 1.4 | D�� | 1.5 |
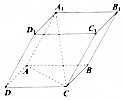 ��ͼ����ƽ��������A1C�У�AD=AB=AA1=4����A1AB=60�㣬��BAD=90�㣬��A1AD=120�㣬cos��A1AC=��������
��ͼ����ƽ��������A1C�У�AD=AB=AA1=4����A1AB=60�㣬��BAD=90�㣬��A1AD=120�㣬cos��A1AC=��������| A�� | -$\frac{\sqrt{3}}{2}$ | B�� | -$\frac{1}{2}$ | C�� | 0 | D�� | $\frac{1}{2}$ |
| A�� | ����ƽ��$\frac{��}{3}$����λ���� | B�� | ����ƽ��$\frac{��}{6}$����λ���� | ||
| C�� | ����ƽ��$\frac{��}{3}$����λ���� | D�� | ����ƽ��$\frac{��}{6}$����λ���� |
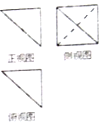 ij�����������ͼ��ͼ��ʾ������ͼ������ͼ��������Ϊ2�ĵ���ֱ�������Σ�����ͼ�DZ߳�Ϊ2�������Σ������������ĸ�������������ֵΪ2$\sqrt{3}$��
ij�����������ͼ��ͼ��ʾ������ͼ������ͼ��������Ϊ2�ĵ���ֱ�������Σ�����ͼ�DZ߳�Ϊ2�������Σ������������ĸ�������������ֵΪ2$\sqrt{3}$��