题目内容
7.已知某水库近50年来年入流量X(单位:亿立方米)的频数分布如表:| 年入流量 | 40<X<80 | 80≤X≤120 | X>120 |
| 年数 | 10 | 35 | 5 |
| 年入流量 | 40<X<80 | 80≤X≤120 | X>120 |
| 最多运行台数 | 1 | 2 | 3 |
(2)若某台发电机组正常运行,则该台发电机组年利润为5000万元;若某台发电机组未运行,则该台发电机组年亏损800万元.为使水电站年总利润的期望达到最大,应安装发电机组多少台?
分析 (1)依题意,先求出随机变量Y的分布列,由此能求出随机变量Y的数学期望.
(2)记水电站总利润为Z(单位:万元),分别求出安装1台发电机、?安装2台发电机、?安装3台发电机的利润的期望,由此得到欲使水电站年总利润的期望达到最大,应安装发电机2台.
解答 解:(1)依题意,${p_1}=p(40<X<80)=\frac{10}{50}=0.2$.
${p_2}=p(80≤X≤120)=\frac{35}{50}=0.7$,
${p_3}=p(X≥120)=\frac{5}{50}=0.1$.
随机变量Y的分布列为
| Y | 1 | 2 | 3 |
| P | 0.2 | 0.7 | 0.1 |
(2)记水电站总利润为Z(单位:万元)
?安装1台发电机的情形.
由于水库年流入量总大于40,故一台发电机运行的概率为1,对应的年利润 Z=5000,E(Z)=5000×1=5000.
?安装2台发电机的情形.
依题意,当40<X<80时,一台发电机运行,此时Z=5000-800=4200,
因此P(Z=4200)=P(40<X<80)=0.2;
当X≥80时,两台发电机运行,此时 Z=5000×2=10000,因此P(Z=10000)=P(X≥80)=0.8.
由此 Z的分布列如下:
| Z | 4200 | 10000 |
| P | 0.2 | 0.8 |
?安装3台发电机的情形.
依题意,当40<X<80时,一台发电机运行,此时Z=5000-1600=3400,因此P(Z=3400)=P(40<X<80)=0.2;
当80≤X≤120时,两台发电机运行,此时 Z=5000×2-800=9200,因此P(Z=9200)=P(80≤X≤120)=0.7.
当X>120时,三台发电机运行,此Z=5000×3=15000,因此P(Z=15000)=P(X>120)=0.1.
由此Z的分布列如下:
| Z | 40<X<80 | 80≤X≤120 | X>120 |
| P | 0.2 | 0.7 | 0.1 |
综上,欲使水电站年总利润的期望达到最大,应安装发电机2台.
点评 本题考查离散型机量的分布和数学期望的求法及应用,正确理解题意是基础,准确写出各分布列是关键.本题考查学生逻辑推理能力和离散随机变量的分布.

练习册系列答案
相关题目
18.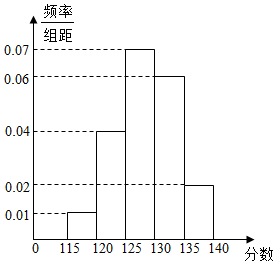 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
(1)若用分层抽样的方法从这500人中抽取20人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的20名学生中,要随机抽取2名学生参加分析座谈会,记其中成绩为优秀的人数为X,求X的分布列及数学期望.
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.(1)若用分层抽样的方法从这500人中抽取20人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的20名学生中,要随机抽取2名学生参加分析座谈会,记其中成绩为优秀的人数为X,求X的分布列及数学期望.
| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
15.已知cosα=-$\frac{1}{2}$,且α是钝角,则tanα等于( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
2.某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 分数区间 | 甲班频率 | 乙班频率 |
| [0,30) | 0.1 | 0.2 |
| [30,60) | 0.2 | 0.2 |
| [60,90) | 0.3 | 0.3 |
| [90,120) | 0.2 | 0.2 |
| [120,150) | 0.2 | 0.1 |
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
| 优秀 | 不优秀 | 总计 | |
| 甲班 | |||
| 乙班 | |||
| 总计 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
12.某市小型机动车驾照“科二”考试共有5项考察项目,分别记作①,②,③,④,⑤
(Ⅰ)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格项目),求补测项目种类不超过3项的概率.
(Ⅱ)“科二”考试中,学员需缴纳150元报名费,并进行1轮测试(按①,②,③,④,⑤的顺序进行),如果某项目不合格,可免费再进行1轮补测,若第1轮补测中仍有不合格项目,可选择“是否补考”,若补考则需缴纳300元补考费,并获得最多2轮补考机会,否则考试结束.每1轮补测都按①,②,③,④,⑤的顺序进行.学员在任何1轮测试或补测中5个项目均合格,方可通过“科二”考试,每人最多只能补考1次.某学员每轮测试或补测通过①,②,③,④,⑤各项测试的概率依次为1,1,1,$\frac{9}{10}$,$\frac{2}{3}$,且他遇到“是否补考”的决断时会选择补考.
(Ⅰ)求该学员能通过“科二”考试的概率.
(Ⅱ)求该学员缴纳的考试费用X的数学期望.
(Ⅰ)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格项目),求补测项目种类不超过3项的概率.
(Ⅱ)“科二”考试中,学员需缴纳150元报名费,并进行1轮测试(按①,②,③,④,⑤的顺序进行),如果某项目不合格,可免费再进行1轮补测,若第1轮补测中仍有不合格项目,可选择“是否补考”,若补考则需缴纳300元补考费,并获得最多2轮补考机会,否则考试结束.每1轮补测都按①,②,③,④,⑤的顺序进行.学员在任何1轮测试或补测中5个项目均合格,方可通过“科二”考试,每人最多只能补考1次.某学员每轮测试或补测通过①,②,③,④,⑤各项测试的概率依次为1,1,1,$\frac{9}{10}$,$\frac{2}{3}$,且他遇到“是否补考”的决断时会选择补考.
(Ⅰ)求该学员能通过“科二”考试的概率.
(Ⅱ)求该学员缴纳的考试费用X的数学期望.
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| (1) | T | T | T | ||
| (2) | T | T | T | ||
| (3) | T | T | T | T | |
| (4) | T | T | T | ||
| (5) | T | T | T | T | |
| (6) | T | T | T | ||
| (7) | T | T | T | T | |
| (8) | T | T | T | T | T |
| (9) | T | T | T | ||
| (10) | T | T | T | T | T |
| 注:“T”表示合格,空白表示不合格 | |||||
16.已知$sinα=-\frac{2}{3}$且α在第三象限,则tan(π+α)等于( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
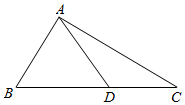 如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.
如图,D是直角△ABC斜边BC上一点,AC=$\sqrt{3}$DC.