题目内容

8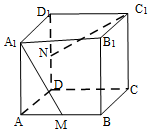．已知正方体ABCD-A1B1C1D1中，M，N分别为棱AB，DD1的中点，异面直线A1M和C1N所成的角为（　　）
A．30°B．45°C．60°D．90°

分析 先通过作平行线的方法作出异面直线所成的角，再在正方形ABB1A1中求解即可．

解答 解：取AA1的中点E，连接B1E，
∵E、N分别是中点，∴EB1∥NC1，
B1E与A1M所成的角是所求的异面直线所成的角                     
在正方形ABB1A1中，M，E分别是边的中点，∴B1E⊥A1M，
则异面直线A1M与C1N所成的角是90°．
故选D．

点评 本题考查异面直线所成的角及空间想象能力，关键是转化为平面角解答．

练习册系列答案
相关题目
18．函数y=lg（1-x）+lg（1+x）是（　　）
A．奇函数，且在（0，1）上是增函数B．奇函数，且在（0，1）上是减函数
C．偶函数，且在（0，1）上是增函数D．偶函数，且在（0，1）上是减函数
19．已知f（x）是一次函数，且满足3f（x+1）-f（x）=2x+9，g（x）是二次函数，且满足g（x）=0，g（x+1）=g（x）+x+1，则：
（1）求函数f（x）的解析式；
（2）求函数g（x）的解析式；
（3）画出h（x）=$\left\{\begin{array}{l}{f（x），x≥-2}\\{g（x），x＜-2}\end{array}\right.$的图象，并根据图象写出h（x）的最小值．
16．若实数x，y满足$\left\{\begin{array}{l}{4x+3y=0}\\{x-y≥-14}\\{x-y≤7}\end{array}\right.$，则$\sqrt{{x}^{2}+{y}^{2}}$的取值范围是（　　）
A．[0，10]B．[0，9]C．[2，10]D．[1，11]
3．若直线l：ax+by=0与圆C：（x-2）2+（y+2）2=8相交，则直线l的倾斜角不等于（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{5π}{6}$
13．△ABC中，cosA=$\frac{1}{8}$，AB=4，AC=2，则∠A的角平分线AD的长为（　　）
A．$2\sqrt{2}$B．$2\sqrt{3}$C．2D．1
20．函数y=（$\frac{1}{2}$）|x|的图象大致为（　　）
A．B．C．D．
17．设a=（$\frac{1}{2}$）0.9，b=（$\frac{1}{2}$）-0.3，c=log30.7，则有（　　）
A．c＜a＜bB．a＜b＜cC．c＜b＜aD．b＜a＜c
18．设$\frac{1}{2}$＜（$\frac{1}{2}$）b＜（$\frac{1}{2}$）a＜1，那么（　　）
A．1＜aa＜abB．aa＜ab＜1C．ab＜aa＜1D．1ab＜aa

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网