设a=0.9.b=-0.3.c=log30.7.则有( )A．c＜a＜bB．a＜b＜cC．c＜b＜aD．b＜a＜c 题目和参考答案——青夏教育精英家教网——

题目内容

17．设a=（$\frac{1}{2}$）^0.9，b=（$\frac{1}{2}$）^-0.3，c=log₃0.7，则有（　　）

A．

c＜a＜b

B．

a＜b＜c

C．

c＜b＜a

D．

b＜a＜c

分析利用指数函数与对数函数的单调性即可得出．

解答解：∵a=（$\frac{1}{2}$）^0.9∈（0，1），b=（$\frac{1}{2}$）^-0.3＞1，c=log₃0.7＜0，
则b＞a＞c．
故选：A．

点评本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案

学生用书系列答案

全优训练系列答案

语文阅读阶梯训练系列答案

巴蜀英才课课练与单元测试系列答案

听力特训营系列答案

智慧万羽中考试题荟萃系列答案

新课标三维同步训练系列答案

海淀黄冈名师导航系列答案

普通高中同步练习册系列答案

同步练习册课时练系列答案

相关题目

7．周期为4的奇函数f（x）在[0，2]上的解析式为f（x）=$\left\{\begin{array}{l}{{x}^{2}，0≤x≤1}\\{lo{g}_{2}x+1，1＜x≤2}\end{array}\right.$，则f（2015）+f（2016）+f（2017）+f（2018）=（　　）

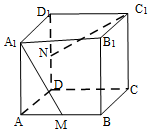已知正方体ABCD-A₁B₁C₁D₁中，M，N分别为棱AB，DD₁的中点，异面直线A₁M和C₁N所成的角为（　　）

5．一种放射性元素，最初的质量为500克，按每年10%衰减．
（1）求t年后，这种放射性元素的质量w的表达式；
（2）用求出的函数表达式，求这种放射性元素的半衰期．（放射性元素的原子核有半数发生衰变时所需要的时间，叫“半衰期”）（lg0.5≈-0.3010，lg0.9≈-0.0458，结果精确到0.1）．

12．函数f（x）=ax⁵-bx+1，若f（lg（log₅10））=5，求f（lg（lg5））的值（　　）

2．已知函数f（x）=x²+bx+1满足f（1+x）=f（1-x），$g（x）=\frac{f（x）}{x}$．
（1）求函数f（x）的解析式；
（2）判断g（x）在[1，2]上的单调性并用定义证明你的结论；
（3）求g（x）在[1，2]上的最大值和最小值．

9．已知函数f（x）=sinx-a（0≤x≤$\frac{5π}{2}$）的三个零点成等比数列，则log₂a=-$\frac{1}{2}$．

6．已知数列{a_n}，它的前n项和为S_n，若a_n=$\frac{1}{（2n+1）（2n-1）}$，则S_n=（　　）

$\frac{2}{2n+1}$

$\frac{2n}{2n+1}$

$\frac{n}{2n+1}$

$\frac{1}{2n+1}$

7．下列说法中，正确的是（　　）

	A．	数列{$\frac{n+1}{n}$} 的第k项为1+$\frac{1}{k}$
	B．	数列0，2，4，6，8…可记为{2n}
	C．	数列1，0，-1与数列-1，0，1是相同的数列
	D．	数列1，3，5，7可表示为{1，3，5，7}