题目内容
19.已知f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9,g(x)是二次函数,且满足g(x)=0,g(x+1)=g(x)+x+1,则:(1)求函数f(x)的解析式;
(2)求函数g(x)的解析式;
(3)画出h(x)=$\left\{\begin{array}{l}{f(x),x≥-2}\\{g(x),x<-2}\end{array}\right.$的图象,并根据图象写出h(x)的最小值.
分析 (1)(2)分别利用待定系数法求函数的解析式即可;
(3)结合(1),(2)可得h(x)的解析式,画出图形,得到最小值.
解答 解:(1)因为f(x)是一次函数,
所以设f(x)=kx+b,k≠0,
∴f(x+1)=k(x+1)+b=kx+k+b,
3f(x+1)-f(x)=3(kx+k+b)-(kx+b)=2kx+3k+2b
因为对任意x,有3f(x+1)-f(x)=2x+9,
所以对任意x,有2kx+3k+2b=2x+9
因此必有$\left\{\begin{array}{l}2k=2\\ 3k+2b=9\end{array}\right.$,解之得:$\left\{\begin{array}{l}k=1\\ b=3\end{array}\right.$
∴f(x)的解析式为:f(x)=x+3.
(2)∵g(x)是二次函数,
所以设g(x)=ax2+bx+c,(a≠0),
$\begin{array}{l}∴g({x+1})=a{({x+1})^2}+b({x+1})+c\\=a{x^2}+({2a+b})x+a+b+c\end{array}$
$\begin{array}{l}g(x)+x+1=a{x^2}+bx+c+x+1\\=a{x^2}+({b+1})x+c+1\end{array}$
∵对任意x,有g(x+1)=g(x)+x+1,
∴对任意x,有ax2+(2a+b)x+a+b+c=ax2+(b+1)x+c+1
因此必有$\left\{\begin{array}{l}2a+b=b+1\\ a+b+c=c+1\end{array}\right.$,解之得:$\left\{\begin{array}{l}a=\frac{1}{2}\\ b=\frac{1}{2}\end{array}\right.$,
∴$g(x)的解析式为:g(x)=\frac{1}{2}{x^2}+\frac{1}{2}x$.
(3)结合(1),(2)可得$h(x)=\left\{\begin{array}{l}x+3,x≥-2\\ \frac{1}{2}{x^2}+\frac{1}{2}x,x<-2\end{array}\right.$,图象如图, h(x)的最小值为h(-2)=1.
h(x)的最小值为h(-2)=1.
点评 本题考查了利用待定系数法求函数解析式以及由函数图象得到函数的最值.属于常规题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案B地区用户满意度评分:92,60,69,70,76,82,70,85,72,87,67,50,91,96,70,82,94,85,75,59,74,89,77,88,78,67,79,94,78,65,64,73,60,75,86,65,90,84,74,80
(1)完成B地区用户满意度评分的频率分布表并作出频率分布直方图;
B地区用户满意度评分的频率分布表
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | |||||
| 频率 |

(2)通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(3)根据用户满意度评分,将用户的满意度分为三个等级:
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
| A. | (-∞,0] | B. | (-∞,1] | C. | (-∞,2] | D. | (-∞,3] |
 函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$,则下列关于函数f(x)的说法中正确的是( )
函数f(x)=Asin(ωx+φ)的图象如图所示,其中A>0,ω>0,|φ|<$\frac{π}{2}$,则下列关于函数f(x)的说法中正确的是( )| A. | 在(-$\frac{3π}{2}$,-$\frac{5π}{6}$)上单调递减 | B. | φ=-$\frac{π}{6}$ | ||
| C. | 最小正周期是π | D. | 对称轴方程是x=$\frac{π}{3}$+2kπ (k∈Z) |
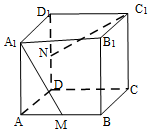 已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )
已知正方体ABCD-A1B1C1D1中,M,N分别为棱AB,DD1的中点,异面直线A1M和C1N所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |