题目内容
10.在△ABC中,角A、B、C的对边分别为a,b,c,且bcosC=(2a-c)cosB.(1)求角B的大小;
(2)已知b=$\sqrt{3}$,BD为AC边上的高,求BD的取值范围.
分析 (1)由bcosC=(2a-c)cosB得a2+c2-b2=ac,∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{1}{2}$,即B=$\frac{π}{3}$.
(2)设BD为AC边上的高为h由s=$\frac{1}{2}acsinB=\frac{1}{2}bh$,得h=$\frac{\sqrt{3}ac}{2b}$=ac,由余弦定理得b2=a2+c2-2accosB3≥2ac-ac,即ac≤3,即h=$\frac{\sqrt{3}ac}{2b}$=ac≤3,从而可得BD的取值范围
解答 解:(1)由bcosC=(2a-c)cosB得b•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=(2a-c)$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
化简得a2+c2-b2=ac,∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{1}{2}$,
∵B∈(0,π),∴B=$\frac{π}{3}$.
(2)设BD为AC边上的高为h,
∵s=$\frac{1}{2}acsinB=\frac{1}{2}bh$,∴h=$\frac{\sqrt{3}ac}{2b}$=ac,
由余弦定理得b2=a2+c2-2accosB⇒a2+c2-ac=3⇒3≥2ac-ac,
∴ac≤3,∴h=$\frac{\sqrt{3}ac}{2b}$=ac≤3.
故BD的取值范围为(0,3]
点评 本题考查了正余弦定理的应用,转化思想,属于中档题.

练习册系列答案
相关题目
1.设向量$\overrightarrow a=({-1,2}),\overrightarrow b=({2,1})$,则$\overrightarrow a+\overrightarrow b$与$\vec b$的夹角为( )
| A. | 45° | B. | 60° | C. | 120° | D. | 135° |
18.某学校食堂推出两款优惠套餐,甲、乙、丙三位同学选择同一款餐的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 向图所示的边长为1的正方形区域内任投一粒豆子,则该豆子落入阴影部分的概率为ln2.
向图所示的边长为1的正方形区域内任投一粒豆子,则该豆子落入阴影部分的概率为ln2.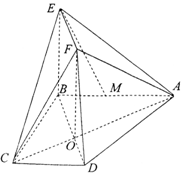 如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.
如图所示,梯形ABCD两条对角线AC,BD的交点为O,AB=2CD,四边形OBEF为矩形,M为线段AB上一点,AM=2MB.