题目内容
18．已知向量$\overrightarrow a=（{m，3}）$，$\overrightarrow b=（{\sqrt{3}，1}）$，若向量$\overrightarrow a$，$\overrightarrow b$的夹角为30°，则实数m=$\sqrt{3}$．分析 利用两个向量的数量积的定义，两个向量的数量积公式，求得m的值．
解答 解：∵$\overrightarrow a=（{m，3}）$，$\overrightarrow b=（{\sqrt{3}，1}）$，向量$\overrightarrow a$，$\overrightarrow b$的夹角为30°，
∴$\overrightarrow{a}•\overrightarrow{b}$=$\sqrt{3}$m+3=$\sqrt{{m}^{2}+9}$•2•cos30°，求得 $m=\sqrt{3}$，
故答案为：$\sqrt{3}$．
点评 题主要考查两个向量的数量积的定义，两个向量的数量积公式的应用，属于基础题．
练习册系列答案
相关题目
8．在数列{an}中，a1=1，a2=2，且${a_{n+2}}-{a_n}=1+{（-1）^n}$（n∈N+），则S100=（ ）
| A． | 0 | B． | 1300 | C． | 2600 | D． | 2602 |
9．在平面直角坐标系中，不等式组$\left\{\begin{array}{l}3x-2y≥0\\ 3x-y-3≤0\\ y≥0\end{array}\right.$表示的平面区域的面积是（ ）
| A． | 1 | B． | $\frac{3}{2}$ | C． | 2 | D． | $\frac{5}{2}$ |
6．设a，b≠0，则“a＞b”是“$\frac{1}{a}＜\frac{1}{b}$”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
13．已知z=m-1+（m+2）i在复平面内对应的点在第二象限，则实数m的取值范围是（ ）
| A． | （-1，2） | B． | （-2，1） | C． | （1，+∞） | D． | （-∞，-2） |
12．已知函数f（x）=（2a-1）x-$\frac{1}{2}$cos2x-a（sinx+cosx）在[0，$\frac{π}{2}$]上单调递增，则实数a的取值范围为（ ）
| A． | （-∞，$\frac{1}{3}$] | B． | [$\frac{1}{3}$，1] | C． | [0，+∞） | D． | [1，+∞） |
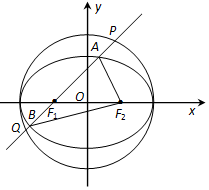如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）过点$（{1\;，\;\frac{3}{2}}）$，两个焦点为F1（-1，0）和F2（1，0）．圆O的方程为x2+y2=a2．