Question

已知函数f（x）=x|m-x|（x∈R），且f（4）=0．
（1）作出函数f（x）的图象，并指出函数f（x）的单调区间；
（2）根据图象写出不等式f（x）＞0的解集；
（3）求当x∈[1，5]时函数的值域．

Answer 1

考点：绝对值不等式的解法,函数的值域,函数的图象与图象变化

专题：不等式的解法及应用

分析：（1）由f（4）=0，求得m=4，函数f（x）=

x(x-4)，x≥4 x(4-x)，x＜4

，由此它的图象如图所示：结合它的图象可得减区间和增区间．
（2）根据图象写出不等式f（x）＞0的解集．
（3）当x∈[1，5]时，结合函数的图象求得函数的值域

解答： 解：（1）由函数f（x）=x|m-x|（x∈R），且f（4）=0，可得4|m-4|=0，
∴m=4，函数f（x）=x|4-x|=

x(x-4)，x≥4 x(4-x)，x＜4

，
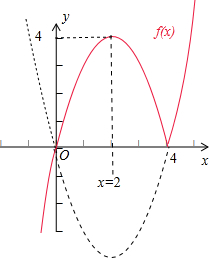
它的图象如图所示：
结合它的图象可得减区间为[2，4]，增区间为（-∞，2）、（4，+∞）．
（2）根据图象写出不等式f（x）＞0的解集为（0，4）∪（4，+∞）．
（3）当x∈[1，5]时，结合函数的图象可得，当x=2时，函数取得最大值为4，
当x=4时，函数取得最小值为0，故函数的值域为[0，4]．

点评：本题主要考查对由绝对值的函数，函数的单调性以及函数的值域，属于基础题．