题目内容
已知A、B、C是直线l上的三点，且|AB|=|BC|=6，⊙O′切直线l于点A，又过B、C作⊙O′异于l的两切线，设这两切线交于点P，求点P的轨迹方程．
考点：轨迹方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：设过B、C异于l的两切线分别切⊙O′于D、E两点，两切线交于点P．由切线的性质，结合椭圆定义知，点P的轨迹是以B、C为两焦点的椭圆，建立坐标系，可求得动点P的轨迹方程．
解答：
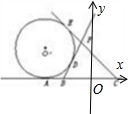解：设过B、C异于l的两切线分别切⊙O′于D、E两点，两切线交于点P．
由切线的性质知：|BA|=|BD|，|PD|=|PE|，|CA|=|CE|，
故|PB|+|PC|=|BD|+|PD|+|PC|=|BA|+|PE|+|PC|=|BA|+|CE|=|AB|+|CA|=6+12=18＞6=|BC|，
故由椭圆定义知，点P的轨迹是以B、C为两焦点的椭圆
以l所在的直线为x轴，以BC的中点为原点，建立坐标系，可求得动点P的轨迹方程为
+
=1（y≠0）
解：设过B、C异于l的两切线分别切⊙O′于D、E两点，两切线交于点P．由切线的性质知：|BA|=|BD|，|PD|=|PE|，|CA|=|CE|，
故|PB|+|PC|=|BD|+|PD|+|PC|=|BA|+|PE|+|PC|=|BA|+|CE|=|AB|+|CA|=6+12=18＞6=|BC|，
故由椭圆定义知，点P的轨迹是以B、C为两焦点的椭圆
以l所在的直线为x轴，以BC的中点为原点，建立坐标系，可求得动点P的轨迹方程为
| x2 |
| 81 |
| y2 |
| 72 |
点评：本题考查轨迹方程，考查椭圆的定义，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=x|m-x|（x∈R），且f（4）=0．
（1）作出函数f（x）的图象，并指出函数f（x）的单调区间；
（2）根据图象写出不等式f（x）＞0的解集；
（3）求当x∈[1，5]时函数的值域．
（1）作出函数f（x）的图象，并指出函数f（x）的单调区间；
（2）根据图象写出不等式f（x）＞0的解集；
（3）求当x∈[1，5]时函数的值域．
动点P（cosθ，sinθ）（θ∈R）关于直线y=x-2的对称点是P′，则|PP′|的最大值（ ）
A、2
| ||
B、
| ||
C、2
| ||
D、2
|
已知Sn为数列{an}的前n项和，且满足a1=1，a2=3，an+1=3an，则S2014=（ ）
| A、2×32014-2 | ||
| B、2×32014 | ||
C、
| ||
D、
|