题目内容
9.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)左右焦点分别为F1,F2,渐近线为l1,l2,P位于l1在第一象限内的部分,若l2⊥PF1,l2∥PF2,则双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{2}$ |
分析 分别求得双曲线的渐近线方程,设P点坐标,根据直线的斜率公式,求得直线PF1的斜率及直线PF2的斜率,根据直线平行及垂直的关系,即可求得a和b的关系,根据双曲线的离心率公式,即可求得双曲线的离心率.
解答 解:设双曲线渐近线为l1的方程y=$\frac{b}{a}$x,渐近线为l2方程y=-$\frac{b}{a}$x,
则设P点坐标(x,$\frac{b}{a}$x),
则直线PF1的斜率k=$\frac{\frac{b}{a}x-0}{x+c}$=$\frac{bx}{a(x+c)}$,
直线PF2的斜率k=$\frac{\frac{b}{a}x}{x-c}$=$\frac{bx}{a(x-c)}$,
由l2⊥PF1,则$\frac{bx}{a(x+c)}$×(-$\frac{b}{a}$)=-1,$\frac{{b}^{2}x}{{a}^{2}(x+c)}$=1,①
l2∥PF2,则$\frac{bx}{a(x-c)}$=-$\frac{b}{a}$,解得:x=$\frac{c}{2}$,②
由①②整理得:$\frac{{b}^{2}}{{a}^{2}}$=3,
由双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=2,
∴双曲线的离心率2,
故选A.
点评 本题考查双曲线的简单几何性质,直线的斜率公式,考查计算能力,属于中档题.

练习册系列答案
相关题目
17.对某工厂生产的产品进行质量监测,现随机抽取该工厂生产的某批次产品中的5件进行检测,测得其中x,y两种指标的含量的数据如下:
(Ⅰ)当该产品中指标x,y满足x≥75且y≥80时,该产品为优等品,求该产品为优等品的概率;
(Ⅱ)若从该产品中随机抽取2件,求出取的2件产品中优等品数的分布列和数学期望.
| 产品编号 | 1 | 2 | 3 | 4 | 5 |
| 指标 x | 69 | 78 | 66 | 75 | 80 |
| 指标 y | 75 | 80 | 77 | 70 | 81 |
(Ⅱ)若从该产品中随机抽取2件,求出取的2件产品中优等品数的分布列和数学期望.
4.椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$短轴的一个端点到其一个焦点的距离是( )
| A. | 5 | B. | 4 | C. | 3 | D. | $\sqrt{7}$ |
19.设复数z满足zi=1-2i,则|z|=( )
| A. | 5 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{2}$ |
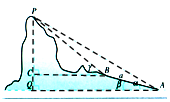 如图,在山脚A测得山顶P的仰角为60°,沿倾斜角为15°的斜坡向上走200米到B,在B处测得山顶P的仰角为75°,则山高h=150($\sqrt{6}$+$\sqrt{2}$)米.
如图,在山脚A测得山顶P的仰角为60°,沿倾斜角为15°的斜坡向上走200米到B,在B处测得山顶P的仰角为75°,则山高h=150($\sqrt{6}$+$\sqrt{2}$)米. 我国齐梁时代的数学家祖暅(公元前5-6世纪,祖冲之之子)提出了一条原理:“幂势既同,则积不容异”,这个原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体,如图,将底面直径都为2b,高皆为a的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面β上,用平行于平面β且与平面β任意距离d处的平面截这两个几何体,可横截得到S圆及S环两截面,可以证明S圆=S环总成立.据此,短轴长为$2\sqrt{3}$,长轴为5的椭球体的体积是10π.
我国齐梁时代的数学家祖暅(公元前5-6世纪,祖冲之之子)提出了一条原理:“幂势既同,则积不容异”,这个原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现,比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体,如图,将底面直径都为2b,高皆为a的椭半球体和已被挖去了圆锥体的圆柱体放置于同一平面β上,用平行于平面β且与平面β任意距离d处的平面截这两个几何体,可横截得到S圆及S环两截面,可以证明S圆=S环总成立.据此,短轴长为$2\sqrt{3}$,长轴为5的椭球体的体积是10π.