题目内容
3.若直线mx+2y+m=0与直线3mx+(m-1)y+7=0平行,则m的值为( )| A. | 7 | B. | 0或7 | C. | 0 | D. | 4 |
分析 由m(m-1)=3m×2,求出m值,再进行检验即可.
解答 解:∵直线mx+2y+m=0与直线3mx+(m-1)y+7=0平行,
∴m(m-1)=3m×2,
∴m=0或7,
经检验都符合题意.
故选:B.
点评 本题考查两直线平行的性质,两直线平行时,一次项系数之比相等,但不等于常数项之比.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
13.抛物线y2=2x的准线方程是( )
| A. | x=$\frac{1}{2}$ | B. | x=1 | C. | x=-$\frac{1}{2}$ | D. | x=-1 |
14.若中心在原点,焦点在y轴上的双曲线离心率为$\sqrt{3}$,则此双曲线的渐近线方程为( )
| A. | y=±x | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | $y=±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
12.已知$\overrightarrow a=({1,cosa}),\overrightarrow b=({sina,1})$,若$\overrightarrow a⊥\overrightarrow b$,则sin2α=( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
12.已知$\overrightarrow{OA}=(1,1,0)$,$\overrightarrow{OB}=(4,1,0)$,$\overrightarrow{OC}=(4,5,-1)$,则向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角的余弦值为( )
| A. | $\frac{{\sqrt{26}}}{26}$ | B. | $\frac{{\sqrt{26}}}{12}$ | C. | $\frac{{3\sqrt{26}}}{26}$ | D. | $\frac{{2\sqrt{26}}}{13}$ |
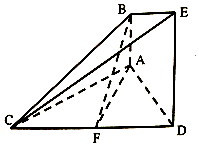 如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.