题目内容
11.圆C1:x2+y2+2ax+a2-9=0和圆C2:x2+y2-4by-1+4b2=0只有一条公切线,若a∈R,b∈R,且ab≠0,则$\frac{4}{a^2}+\frac{1}{b^2}$的最小值为4.分析 由题意可得两圆相内切,根据两圆的标准方程求出圆心和半径,可得a2+4b2=4,再利用“1”的代换,使用基本不等式求得$\frac{4}{a^2}+\frac{1}{b^2}$的最小值.
解答 解:由题意可得两圆相内切,两圆的标准方程分别为 (x+a)2+y2=9,x2+(y-2b)2=1,
圆心分别为(-a,0),(0,2b),半径分别为3和1,故有$\sqrt{{a}^{2}+4{b}^{2}}$=2,∴a2+4b2=4,
∴$\frac{4}{a^2}+\frac{1}{b^2}$=$\frac{1}{4}$($\frac{4}{a^2}+\frac{1}{b^2}$)(a2+4b2)=$\frac{1}{4}$(8+$\frac{16{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$)≥4,
当且仅当$\frac{16{b}^{2}}{{a}^{2}}$=$\frac{{a}^{2}}{{b}^{2}}$时,等号成立,
∴$\frac{4}{a^2}+\frac{1}{b^2}$的最小值为4.
故答案为:4.
点评 本题考查两圆的位置关系,两圆相内切的性质,圆的标准方程的特征,基本不等式的应用,得到a2+4b2=4是解题的关键和难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设函数f(x)=sin(ωx+φ)(φ>0)的图象关于直线x=-1和x=2对称,则f(0)的取值集合是( )
| A. | {-1,1,-$\frac{1}{2}$} | B. | {1,-$\frac{1}{2}$,$\frac{1}{2}$} | C. | {-1,1,-$\frac{1}{2}$,$\frac{1}{2}$} | D. | {-1,1,-2,2} |
6.已知向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=1$,$|\overrightarrow a+\overrightarrow b|=\sqrt{7}$,$\overrightarrow a•(\overrightarrow b-\overrightarrow a)=-4$,则$\overrightarrow a$与$\overrightarrow b$夹角是( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
16.已知$\frac{\overline z}{1+2i}=2+i$,则复数z+5的实部与虚部的和为( )
| A. | 10 | B. | -10 | C. | 0 | D. | -5 |
20.某十字路口的信号灯为红灯和绿灯交替出现,红灯持续的时间为60秒,小明放学回家途经该路口遇到红灯,则小明至少要等15秒才能出现绿灯的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
1.若函数f(x)=(x-1)(x+2)(x2+ax+b)的图象关于直线x=0对称,则f(x)的最小值为( )
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
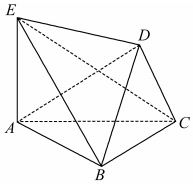 如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.
如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.