题目内容
复数z满足（z-i）i=2+i，则
=（ ）
. |
| z |
| A、-1-i | B、1-i |
| C、-1+3i | D、1+i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：设z=a+bi，由（z-i）i=2+i，求出z=1-i，由此能求出
．
. |
| z |
解答：
解：设z=a+bi，
∵（z-i）i=2+i，
∴[a+（b-1）i]i
=ai+（b-1）i2
=（1-b）+ai
=2+i，
∴
解得a=1，b=-1，
∴z=1-i，
∴
=1+i．
故选：D．
∵（z-i）i=2+i，
∴[a+（b-1）i]i
=ai+（b-1）i2
=（1-b）+ai
=2+i，
∴
|
∴z=1-i，
∴
. |
| z |
故选：D．
点评：本题考查复数的共轭复数的求法，是基础题，解题时要认真审题，注意复数的代数形式的乘除运算的运算公式的合理运用．
练习册系列答案
相关题目
一质点的运动方程是s=4-2t2，则在时间段[1，1+△t]内相应的平均速度为（ ）
| A、2△t+4 |
| B、-2△t+4 |
| C、2△t-4 |
| D、-2△t-4 |
已知椭圆x2sinα-y2cosα=1（0≤α＜2π）的焦点在y轴上，则α的取值范围是（ ）
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
已知直线l1：x+ay+1=0，直线l2：ax+y+2=0，则命题“若a=1或a=-1，则直线l1与l2平行”的否命题为（ ）
| A、若a≠1且a≠-1，则直线l1与l2不平行 |
| B、若a≠1或a≠-1，则直线l1与l2不平行 |
| C、若a=1或a=-1，则直线l1与l2不平行 |
| D、若a≠1或a≠-1，则直线l1与l2平行 |
函数y=xcosx是（ ）
| A、奇函数 | B、偶函数 |
| C、既奇又偶 | D、非奇非偶 |
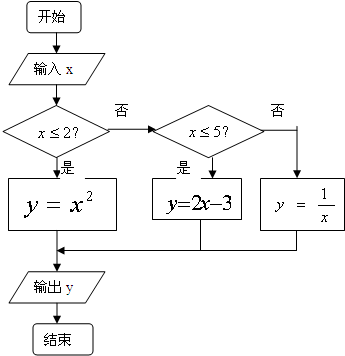如图：