题目内容
4.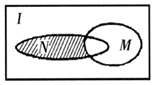 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
分析 由图形可得阴影部分所表示的集合为N∩(CIM)故先化简两个集合,再根据交集的定义求出阴影部分所表示的集合.
解答 解:由题意M={x|x≥3}与N={x|(x-3)(x-1)≤0}={x|1≤x≤3}
由图知阴影部分所表示的集合为N∩(CIM)
∴N∩(CIM)={x|1≤x<3}
故选B.
点评 本题考查Venn图表达集合的关系及运算,解题的关键是根据图象得出N∩(CIM),再由集合的运算求出阴影部分所表示的集合.

练习册系列答案
相关题目
12.已知f(x)=tan(2x+$\frac{π}{4}$),则使f(x)≥$\sqrt{3}$成立的x的集合是( )
| A. | [$\frac{π}{24}$+$\frac{1}{2}$kπ,$\frac{π}{8}$+$\frac{1}{2}$kπ),k∈Z | B. | (-$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{π}{24}$+$\frac{1}{2}$kπ),k∈Z | ||
| C. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ),k∈Z | D. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ],k∈Z |
19.如图所示是y=Asin(ωx+φ)(A>0,ω>0)的图象的一段,它的一个解析式为( ) 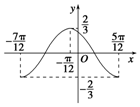

| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
13.函数$y=\frac{1}{3}{x^3}+b{x^2}+(b+2)x+3$在R上不是单调增函数则b范围为( )
| A. | (-1,2) | B. | (-∞,-1]∪[2,+∞) | C. | [-1,2] | D. | (-∞,-1)∪(2,+∞) |
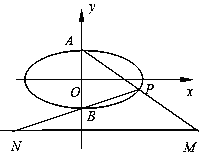 如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,
如图,已知椭圆$C:\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线l:y=-2分别交于点M,N,